
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若曲线![]() 在点
在点![]() 处的切线
处的切线![]() 与曲线
与曲线![]() 切于点
切于点![]() ,求
,求![]() 的值;
的值;
(Ⅲ)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先明确函数定义域,再求函数导数![]() ,根据导函数符号确定单调区间,(2)由导数几何意义得切线斜率为
,根据导函数符号确定单调区间,(2)由导数几何意义得切线斜率为![]() ,则得
,则得![]() ,
, ![]() .即得
.即得![]() (3)不等式恒成立问题,一般转化为对应函数
(3)不等式恒成立问题,一般转化为对应函数![]() 最值问题:先利用导数研究函数最值:
最值问题:先利用导数研究函数最值: ![]() 当
当![]() 时,
时, ![]() 在
在![]() 上单调递增. 仅当
上单调递增. 仅当![]() 时满足条件,此时
时满足条件,此时![]() ;当
;当![]() 时,
时, ![]() 先减后增,
先减后增, ![]() ,再变量分离转化为
,再变量分离转化为![]() ,最后利用导数研究函数
,最后利用导数研究函数
![]() 最值,可得
最值,可得![]() 的最大值.
的最大值.
试题解析:解:(Ⅰ) ![]() ,则
,则![]() .
.
令![]() 得
得![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
令![]() 得
得![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
(Ⅱ)因为![]() ,所以
,所以![]() ,所以
,所以![]() 的方程为
的方程为![]() .
.
依题意, ![]() ,
, ![]() .
.
于是![]() 与抛物线
与抛物线![]() 切于点
切于点![]() ,
,
由![]() 得
得![]() .
.
所以![]()
(Ⅲ)设![]() ,则
,则![]() 恒成立.
恒成立.
易得![]()
(1)当![]() 时,
时,
因为![]() ,所以此时
,所以此时![]() 在
在![]() 上单调递增.
上单调递增.
①若![]() ,则当
,则当![]() 时满足条件,此时
时满足条件,此时![]() ;
;
②若![]() ,取
,取![]() 且
且![]()
此时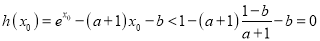 ,所以
,所以![]() 不恒成立.
不恒成立.
不满足条件;
(2)当![]() 时,
时,
令![]() ,得
,得![]() 由
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
要使得“![]() 恒成立”,必须有
恒成立”,必须有
“当![]() 时,
时, ![]() ”成立.
”成立.
所以![]() .则
.则![]()
令![]() 则
则![]()
令![]() ,得
,得![]() 由
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() 所以
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以,当![]() 时,
时, ![]()
从而,当![]() 时,
时, ![]() 的最大值为
的最大值为![]() .
.
综上, ![]() 的最大值为
的最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】二次函数![]() 的图象顶点为
的图象顶点为![]() ,且图象在
,且图象在![]() 轴上截得的线段长为8.
轴上截得的线段长为8.
(1)求函数![]() 的解析式;
的解析式;
(2)令![]() .
.
(ⅰ)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(ⅱ)若![]() 时,不等式
时,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着节能减排意识深入人心,共享单车在各大城市大范围推广,越来越多的市民在出行时喜欢选择骑行共享单车.为了研究广大市民在共享单车上的使用情况,某公司在我市随机抽取了100名用户进行调查,得到如下数据:
每周使用次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)如果用户每周使用共享单车超过3次,那么认为其“喜欢骑行共享单车”.请完成下面的2×2列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关;
不喜欢骑行共享单车 | 喜欢骑行共享单车 | 合计 | |
男 | |||
女 | |||
合计 |
(2)每周骑行共享单车6次及6次以上的用户称为“骑行达人”,将频率视为概率,在我市所有的“骑行达人”中随机抽取4名,求抽取的这4名“骑车达人”中,既有男性又有女性的概率.
附表及公式: ,其中
,其中![]() ;
;
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD⊥平面PCD,PD⊥CD,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2AB, ![]() 为棱PC上一点.
为棱PC上一点.
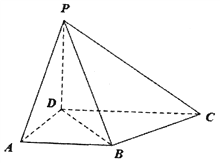
(Ⅰ)若点![]() 是PC的中点,证明:B
是PC的中点,证明:B![]() ∥平面PAD;
∥平面PAD;
(Ⅱ) ![]() 试确定
试确定![]() 的值使得二面角
的值使得二面角![]() -BD-P为60°.
-BD-P为60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当生物死亡后,其体内原有的碳14的含量大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.2019年7月6日,第43届世界遗产大会宣布,中国良渚古城遗址成功申遗,获准列入世界遗产名录.目前中国世界遗产总数已达55处,位居世界第一.今年暑期,某中学的“考古学”兴趣小组对良渚古城水利系统中一条水坝的建筑材料(草裹泥)上提取的草茎遗存进行碳14年代学检测,检测出碳14的残留量约为初始量的54%.利用参考数据:![]() ,请你推断上述所提取的草茎遗存物距今大约有_______________________年(精确到1年).
,请你推断上述所提取的草茎遗存物距今大约有_______________________年(精确到1年).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一则“清华大学要求从 2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.其实,已有不少高校将游泳列为必修内容.
某中学拟在高一-下学期开设游泳选修课,为了了解高--学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(1).请将上述列联表![]() 补充完整,并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
补充完整,并判断是否可以在犯错误的概率不超过0.001的前提下认为喜欢游泳与性别有关.
(2)已知在被调查的学生中有6名来自高一(1) 班,其中4名喜欢游泳,现从这6名学生中随机抽取2人,求恰有1人喜欢游泳的概率.
附:![]()
| 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 /td> | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com