
【题目】已知函数f(x)=sin(x﹣φ),且 ![]() f(x)dx=0,则函数f(x)的图象的一条对称轴是( )
f(x)dx=0,则函数f(x)的图象的一条对称轴是( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
【答案】A
【解析】解:∵函数f(x)=sin(x﹣φ), ![]() f(x)dx=﹣cos(x﹣φ)
f(x)dx=﹣cos(x﹣φ) ![]() =﹣cos(
=﹣cos( ![]() ﹣φ)﹣[﹣cos(﹣φ)]=
﹣φ)﹣[﹣cos(﹣φ)]= ![]() cosφ﹣
cosφ﹣ ![]() sinφ=
sinφ= ![]() cos(φ+
cos(φ+ ![]() )=0,
)=0,
∴φ+ ![]() =kπ+
=kπ+ ![]() ,k∈z,即 φ=kπ+
,k∈z,即 φ=kπ+ ![]() ,k∈z,故可取φ=
,k∈z,故可取φ= ![]() ,f(x)=sin(x﹣
,f(x)=sin(x﹣ ![]() ).
).
令x﹣ ![]() =kπ+
=kπ+ ![]() ,求得 x=kπ+
,求得 x=kπ+ ![]() ,k∈Z,
,k∈Z,
则函数f(x)的图象的一条对称轴为 x= ![]() ,
,
故选:A.
【考点精析】根据题目的已知条件,利用定积分的概念和函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握定积分的值是一个常数,可正、可负、可为零;用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】当x∈[﹣2,1]时,不等式ax3﹣x2+4x+3≥0恒成立,则实数a的取值范围是( )
A.[﹣5,﹣3]
B.[﹣6,﹣ ![]() ]
]
C.[﹣6,﹣2]
D.[﹣4,﹣3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.
(1)大气污染可引起心悸、呼吸困难等心肺疾病. 为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
问有多大的把握认为是否患心肺疾病与性别有关?
(2)空气质量指数PM2.5(单位:μg/![]() )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重. 某市在2016年年初着手治理环境污染,改善空气质量,检测到2016年1~5月的日平均PM2.5指数如下表:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重. 某市在2016年年初着手治理环境污染,改善空气质量,检测到2016年1~5月的日平均PM2.5指数如下表:
月份x | 1 | 2 | 3 | 4 | 5 |
PM2.5指数y | 79 | 76 | 75 | 73 | 72 |
试根据上表数据,求月份x与PM2.5指数y的线性回归直线方程![]() ,并预测2016年8月份的日平均PM2.5指数 (保留小数点后一位).
,并预测2016年8月份的日平均PM2.5指数 (保留小数点后一位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 若对任意的正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 为
为![]() 的中点,且有
的中点,且有![]() ,现以
,现以![]() 为折痕,将
为折痕,将![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
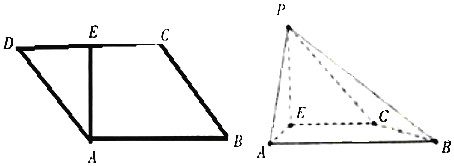
(1)证明:![]() 平面
平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com