
【题目】给出下列五个命题:①“若![]() ,则
,则![]() 或
或![]() ”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为
”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为![]() 的有48对;③“
的有48对;③“ ![]() ”是方程
”是方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线的充分不必要条件;④点
轴上的双曲线的充分不必要条件;④点![]() 是曲线
是曲线![]() (
(![]() ,
, ![]() )上的动点,且满足
)上的动点,且满足![]() ,则
,则![]() 的取值范围是
的取值范围是![]() ;⑤若随机变量
;⑤若随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .其中正确命题的序号是__________(请把正确命题的序号填在横线上).
.其中正确命题的序号是__________(请把正确命题的序号填在横线上).
【答案】②④⑤
【解析】“若![]() ,则
,则![]() 或
或![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() 且
且![]() ,则
,则![]() ”为真,故“若
”为真,故“若![]() ,则
,则![]() 或
或![]() ”为真命题,故①错误;正方体的面对角线共有
”为真命题,故①错误;正方体的面对角线共有![]() 条,两条为一对,共有
条,两条为一对,共有![]() 条,同一面上的对角线不满足题意,对面的面对角线也不满足题意,一组平行平面共有
条,同一面上的对角线不满足题意,对面的面对角线也不满足题意,一组平行平面共有![]() 对不满足题意的直线对数,不满足题意的共有
对不满足题意的直线对数,不满足题意的共有![]() ,从正方体六个面的对角线中任取两条作为一对.其中所成的角为
,从正方体六个面的对角线中任取两条作为一对.其中所成的角为![]() 的共有
的共有![]() ,故②正确;若
,故②正确;若![]() ,则
,则![]() ,故方程
,故方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线,若方程
轴上的双曲线,若方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线,则
轴上的双曲线,则![]() ,得
,得![]() ,故“
,故“![]() ”是方程
”是方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线的充要条件,即③不正确;由
轴上的双曲线的充要条件,即③不正确;由![]() (
(![]() ,
, ![]() ),分类讨论:当
),分类讨论:当![]() 时,化为
时,化为![]() ;当
;当![]() ,
, ![]() 时,化为
时,化为![]() ;当
;当![]() ,
, ![]() 时,化为
时,化为![]() ;当
;当![]() ,
, ![]() 时,化为
时,化为![]() 画出图象:其轨迹为四边形
画出图象:其轨迹为四边形![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,变形为
,变形为![]() ,上式表示点
,上式表示点![]() ,
, ![]() 与图象上的点
与图象上的点![]() 的距离之和
的距离之和![]() ,∴
,∴ ,化为
,化为![]() ,
, ![]() ,
,
∴![]() ,其取值范围为
,其取值范围为![]() ,故④正确;随机变量
,故④正确;随机变量![]() 服从正态分布
服从正态分布![]() ,∵
,∵![]()
![]() ,∴
,∴![]() 与
与![]() 关于
关于![]() 对称,∴
对称,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,故⑤正确;故答案为②④⑤.
,故⑤正确;故答案为②④⑤.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某单位有工程师6人,技术员12人,技工18人,要从这些人中取一个容量为n的样本;如果采用系统抽样和分层抽样方法抽取,无须剔除个体;如果样本容量增加1个,则在采用系统抽样时需要在总体中先剔除一个个体,则n的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①若α、β为第一象限角,且α>β,则sinα>sinβ
②函数y=|sinx|与y=|tanx|的最小正周期相同
③函数f(x)=sin(x+ ![]() )在[﹣
)在[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
④若函数f(x)=asinx﹣bcosx的图象的一条对称轴为直线x= ![]() ,则a+b=0.
,则a+b=0.
其中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() 、
、![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 、
、![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() :
: ![]()
![]() (
(![]() ,
, ![]() )的一条直径的两个端点.
)的一条直径的两个端点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() 、
、![]() .试探究:是否存在数集
.试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是![]() ,
, ![]() 是
是![]() 的中点.
的中点.
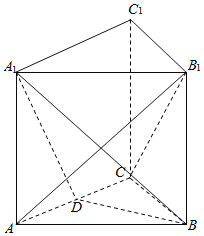
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ) ![]() 图象上的任意两点,且角φ的终边经过点
图象上的任意两点,且角φ的终边经过点 ![]() ,若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
,若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() .
.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间;
(3)当 ![]() 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com