Question

已知函数f（x）是偶函数，当x∈[0，+∞）时f（x）=x³-2x²+x+a，则当a＜0时，方程f（x）=0的根的个数可能是（ ）
A．2、4 个
B．2、6 个
C．2、4、6个
D．0、2、4个

Answer 1

【答案】分析：先考虑当x∈[0，+∞），a＜0时，方程f（x）=0的根的个数，令 g（x）=x³-2x²+x，则 f（x）=g（x）-（-a），
即把函数g（x）的图象向下平移-a个单位得到f（x）的图象．画出函数g（x）的简图，数形结合求得g（x）的零点个数，
即可求得函数g（x）的零点个数．
解答：解：∵函数f（x）是偶函数，当x∈[0，+∞）时，f（x）=x³-2x²+x+a，
先考虑当x∈[0，+∞）且a＜0时，方程f（x）=0的根的个数（即函数f（x）的零点个数）．
令 g（x）=x³-2x²+x=x•（x-1）²，则 f（x）=g（x）-（-a），
即把函数g（x）的图象向下平移-a个单位得到f（x）的图象．
而函数g（x）在[0，+∞）上的零点有2个：即 0 和1，如图所示：

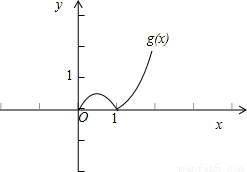
故当x∈[0，+∞）且a＜0 时，方程f（x）=0的根的个数可能为1，2，3，
故当x∈（-∞，+∞）时，由函数f（x）是偶函数，图象关于y轴对称，
可得方程f（x）=0的根的个数可能为2，4，6，
故选C．
点评：本题主要考查方程根的存在性及个数判断，函数的奇偶性、函数的零点，体现了数形结合以及等价转化的数学思想，
属于中档题．