
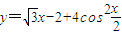 在区间
在区间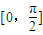 上的最大值是 .
上的最大值是 . 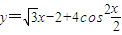
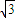 x-2+2(1+cosx)
x-2+2(1+cosx)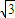 x+2cosx,
x+2cosx, -2sinx,
-2sinx,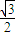 ,又x∈
,又x∈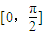 ,∴x=
,∴x=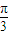 ,
,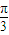 时,y′>0,函数为增函数;
时,y′>0,函数为增函数;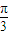 ≤x<
≤x<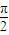 时,y′<0,函数为减函数,
时,y′<0,函数为减函数,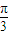 时,函数取最大值,最大值为
时,函数取最大值,最大值为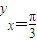 =
=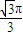 +1.
+1. +1
+1

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:2014届陕西省高二上学期期末考试文科数学试卷(解析版) 题型:解答题
已知 其中
其中 .(1)求函数
.(1)求函数 的单调区间;(2)若函数
的单调区间;(2)若函数 在区间
在区间 内恰有两个零点,求
内恰有两个零点,求 的取值范围;
的取值范围;
(3)当 时,设函数
时,设函数 在区间
在区间 上的最大值为
上的最大值为 最小值为
最小值为 ,记
,记 ,求函数
,求函数 在区间
在区间 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源:2010年江西省高一上学期第一次月考数学卷 题型:解答题
(本题满分10分)
已知函数 且
且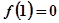 .
.
(1)若函数 是偶函数,求函数
是偶函数,求函数 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(2)要使函数 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省泰兴市高三上学期第一次检测理科数学试题 题型:解答题
(本题满分16分)设二次函数 在区间
在区间 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合 .
.
(1)若 ,且
,且 ,求M和m的值;
,求M和m的值;
(2)若 ,且
,且 ,记
,记 ,求
,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com