
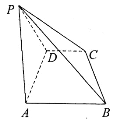
【题目】如图,在四棱锥![]() 中,底面ABCD为梯形,AB//CD,
中,底面ABCD为梯形,AB//CD,![]() ,AB=AD=2CD=2,△ADP为等边三角形.
,AB=AD=2CD=2,△ADP为等边三角形.
(1)当PB长为多少时,平面![]() 平面ABCD?并说明理由;
平面ABCD?并说明理由;
(2)若二面角![]() 大小为150°,求直线AB与平面PBC所成角的正弦值.
大小为150°,求直线AB与平面PBC所成角的正弦值.
【答案】(1)当![]() 时,平面
时,平面![]() 平面
平面![]() ,详见解析(2)
,详见解析(2)![]()
【解析】
(1)根据平面和平面垂直可得线面垂直,从而可得![]() ,利用直角三角形知识可得
,利用直角三角形知识可得![]() 的长;
的长;
(2)构建空间直角坐标系,利用法向量求解直线AB与平面PBC所成角的正弦值.
解:(1)当![]() 时,平面
时,平面![]() 平面
平面![]() ,
,
证明如下:在![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)分别取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,因为
,因为![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,所以
,所以![]() ,故
,故![]() 为二面角
为二面角![]() 的平面角,所以
的平面角,所以![]() ,
,
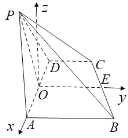
如图,分别以![]() 的方向以及垂直于平面
的方向以及垂直于平面![]() 向上的方向作为
向上的方向作为![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() .
.
可得![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,则有
的一个法向量,则有![]() ,
,
即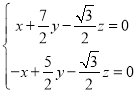 ,令
,令![]() ,
,
可得![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则有
,则有![]()
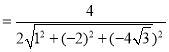
![]()
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付,是指允许用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.随着信息技术的发展,手机支付越来越成为人们喜欢的支付方式.某机构对某地区年龄在15到75岁的人群“是否使用手机支付”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用手机支付的人数如下所示:(年龄单位:岁)
年龄段 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
使用人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“使用手机支付”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | |
使用手机支付 | ||
不使用手机支付 |
(2)若从年龄在[55,65),[65,75]的样本中各随机选取2人进行座谈,记选中的4人中“使用手机支付”的人数为X,求随机变量X的分布列和数学期望.
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
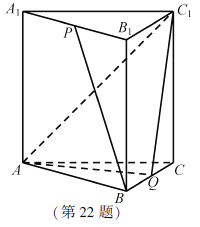
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学经典名著,其中有这样一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有-圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该木材,锯口深一寸,锯道长-尺.问这块圆柱形木材的直径是多少?现有长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙体中的体积约为__________立方寸.(结果保留整数)
寸,估算该木材镶嵌在墙体中的体积约为__________立方寸.(结果保留整数)
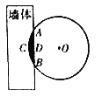
注:l丈=10尺=100寸,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是中国成立70周年,也是全面建成小康社会的关键之年.为了迎祖国70周年生日,全民齐心奋力建设小康社会,某校特举办“喜迎国庆,共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手答题得分情况,则下列说法正确的是( )
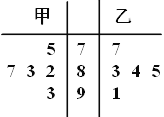
A.甲组选手得分的平均数小于乙组选手的平均数B.甲组选手得分的中位数大于乙组选手的中位数
C.甲组选手得分的中位数等于乙组选手的中位数D.甲组选手得分的方差大于乙组选手的的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com