练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （12分）如图，在直三棱柱中，，，为的中点.（1）求证：⊥平面；（2）设是上一点，试确定的位置，使平面⊥平面，并说明理由.
    （I）∵AB=B1B
    ∴四边形ABB1A1为正方形
    ∴A1B⊥AB1
    又∵AC1⊥面A1BD
    ∴AC1⊥A1B∴A1B⊥面AB1C1  
    ∴A1B⊥B1C1
    又在直棱柱ABC—A1B1C1中BB1⊥B1C1
    ∴B1C1⊥平面ABB1A1                                             
    （II）当点E为C1C的中点时，平面A1BD⊥平面BDE                 
    ∵D、E分别为AC、C1C的中点
    ∴DE∥AC1    ∵AC1⊥平面A1BD
    ∴DE⊥平面A1BD
    又DE平面BDE
    ∴平面A1BD⊥平面BDE                                            
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    对于互不相同的直线和平面，给出下列三个命题：
    ①若与为异面直线，，则∥；
    ②若∥，，则∥；
    ③若，∥，则∥.
    其中真命题的个数为(　　)
    A．3B．2C．1D．0

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分）如图，为等边三角形，为矩形，平面平面，，分别为、、中点，．
    （Ⅰ）求证：
    （Ⅱ）求多面体的体积

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分）
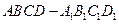
    如图5，是棱长为2 cm的正方体.

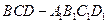
    (I) 求多面体的体积；
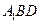
    (II) 求点A到平面的距离；
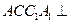
    (Ⅲ) 求证：平面平面.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设三棱锥的顶点在底面内射影在内部，且到三个侧
    面的距离相等，则是的(　　)
    A．外心B．垂心C．内心D．重心

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    如图，棱柱的侧面是菱形，。
    （1）证明：平面；
    （2）设D是上的点且，求的值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）如图，在直三棱柱中，平面侧面．
    （Ⅰ）求证：；
    （Ⅱ）若直线与平面所成角是，锐二面角的平面角是，试判断与的大小关系，并予以证明．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在四面体中，三组对棱棱长分别相等且依次为、、15，则此四面体的外接球的体积为________

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    （右图）已知正方体,E是C1B与CB1的交点，F是BB1的中点，则直线D1E与AF所成角的余弦值的大小为        。

    查看答案和解析>>

    同步练习册答案