
【题目】在三棱柱![]() 中,已知侧棱
中,已知侧棱![]() 底面
底面![]() 为
为![]() 的中点,
的中点, ![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找,往往从两个方面出发,一是利用线面垂直性质定理得线线垂直,二是利用平几知识,结合勾股定理得线线垂直,(2)求点到直线距离,往往利用等体积法求高得到.
试题解析:
解:(1) 证明:在![]() 中,
中, ![]() 为
为![]() 的中点,故
的中点,故![]() ,又侧棱
,又侧棱![]() 底面
底面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,则
,则![]() ,在
,在![]() 中,
中,
![]() ;在
;在![]() 中,
中, ![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
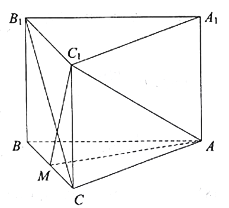
(2)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由于
,由于![]() ,即
,即![]() ,于是
,于是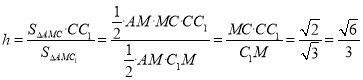 ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
点睛:利用等积法可以用来求解几何图形的高或几何体的高或内切球的半径,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.


科目:高中数学 来源: 题型:
【题目】若f(x)是定义在R上的增函数,下列函数中
①y=[f(x)]2是增函数;
②y= ![]() 是减函数;
是减函数;
③y=﹣f(x)是减函数;
④y=|f(x)|是增函数;
其中正确的结论是( )
A.③
B.②③
C.②④
D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期“共享单车”在全国多个城市持续升温,某移动互联网机构通过对使用者的调查得出,现在市场上常见的八个品牌的“共享单车”的满意度指数如茎叶图所示:
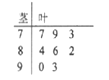
(Ⅰ)求出这组数据的平均数和中位数;
(Ⅱ)某用户从满意度指数超过80的品牌中随机选择两个品牌使用,求所选两个品牌的满意度指数均超过85的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3.定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤1},则A中所有元素的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 在
在![]() 单调递增,其中
单调递增,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,当
,当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小关系(其中
的大小关系(其中![]() 是
是![]() 的导函数),请写出详细的推理过程;
的导函数),请写出详细的推理过程;
(3)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com