
【题目】已知函数f(x)=|x-1|.
(Ⅰ)解不等式f(x)+f(x+4)≥8;
(Ⅱ)若|a|<1,|b|<1,且a≠0,求证:f(ab)>|a|f(![]() ).
).
【答案】(Ⅰ){x|x≤-5,或x≥3}(Ⅱ)见解析
【解析】试题分析:(Ⅰ)易求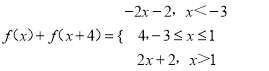 ,利用一次函数的单调性可求
,利用一次函数的单调性可求![]() 的解集;
的解集;
(Ⅱ)![]() 作差证明即可.
作差证明即可.
试题解析:(Ⅰ)f(x)+f(x+4)=|x-1|+|x+3|=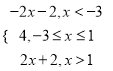 ,
,
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3.
所以不等式的解集为{x|x≤-5,或x≥3}.
(Ⅱ)f(ab)>|a|f(![]() )即|ab-1|>|a-b|.
)即|ab-1|>|a-b|.
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|.
故所证不等式成立.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】某市拟招商引资兴建一化工园区,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如表所示:
支持 | 保留 | 不支持 | |
30岁以下 | 900 | 120 | 280 |
30岁以上(含30岁) | 300 | 260 | 140 |
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在30岁以上的人有多少人被抽取;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=![]() AD=1,CD=
AD=1,CD=![]() .
.
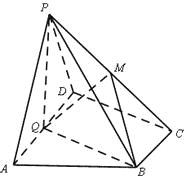
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点.

(Ⅰ)求证:PC∥平面EBD;
(Ⅱ)求证:平面PBC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地棚户区改造建筑用地平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形ABCD是原棚户区建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
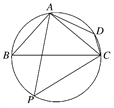
(1)请计算原棚户区建筑用地ABCD的面积及AC的长;
(2)因地理条件的限制,边界AD,DC不能变更,而边界AB,BC可以调整,为了提高棚户区建筑用地的利用率,请在![]() 上设计一点P,使得棚户区改造后的新建筑用地APCD的面积最大,并求出最大值.
上设计一点P,使得棚户区改造后的新建筑用地APCD的面积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表.
非一线 | 一线 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
由K2= ,得K2=
,得K2=![]() .
.
参照下表,
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
正确的结论是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C. 有99%以上的把握认为“生育意愿与城市级别有关”
D. 有99%以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD′E的位置,使得平面AD′E⊥平面ABCE.
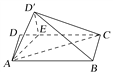
(1)求证:AE⊥BD′;
(2)求三棱锥A-BCD′的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届江苏省泰州中学高三12月月考】已知椭圆的中心为坐标原点![]() ,椭圆短轴长为
,椭圆短轴长为![]() ,动点
,动点![]() (
(![]() )在椭圆的准线上.
)在椭圆的准线上.
(1)求椭圆的标准方程;
(2)求以![]() 为直径且被直线
为直径且被直线![]() 截得的弦长为
截得的弦长为![]() 的圆的方程;
的圆的方程;
(3)设![]() 是椭圆的右焦点,过点
是椭圆的右焦点,过点![]() 作
作![]() 的垂线与以
的垂线与以![]() 为直径的圆交于点
为直径的圆交于点![]() ,求证:线段
,求证:线段![]() 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com