
【题目】如图,已知椭圆![]() ,直线
,直线![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,点
,点![]() 和点
和点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.

(1)若点![]() 是椭圆
是椭圆![]() 的一个焦点,求该椭圆的长轴的长度;
的一个焦点,求该椭圆的长轴的长度;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求证:
,求证:![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】选修4-4坐标系与参数方程选讲
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为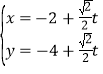 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的平面直角坐标方程和直线
的平面直角坐标方程和直线![]() 的普通方程:
的普通方程:
(2)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题(1)![]() 条斜线段长相等,则他们在平面内的射影长也相等;(2)直线
条斜线段长相等,则他们在平面内的射影长也相等;(2)直线![]() 不在平面
不在平面![]() 内,他们在平面
内,他们在平面![]() 内的射影是两条平行直线,则
内的射影是两条平行直线,则![]() ;(3)与同一平面所成的角相等的两条直线平行;(4)一条直线与一个平面所成的角是
;(3)与同一平面所成的角相等的两条直线平行;(4)一条直线与一个平面所成的角是![]() ,那么它与平面内任何其他直线所成的角都不小于
,那么它与平面内任何其他直线所成的角都不小于![]() ;其中正确的命题序号是____________.
;其中正确的命题序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个创业青年租用一块边长为4百米的等边![]() 田地
田地![]() 如图
如图![]() 养蜂、产蜜与售蜜,田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在CN上,
养蜂、产蜜与售蜜,田地内拟修建笔直小路MN,AP,其中M,N分别为AC,BC的中点,点P在CN上,![]() 规划在小路MN与AP的交点O(O与M、N不重合
规划在小路MN与AP的交点O(O与M、N不重合![]() 处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区,A,N为出入口
处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区,A,N为出入口![]() 小路的宽度不计
小路的宽度不计![]() 为节约资金,小路MO段与OP段建便道,供蜂源植物培育之用,费用忽略不计
为节约资金,小路MO段与OP段建便道,供蜂源植物培育之用,费用忽略不计![]() 为车辆安全出入,小路AO段的建造费用为每百米5万元,小路ON段的建造费用为每百米4万元.
为车辆安全出入,小路AO段的建造费用为每百米5万元,小路ON段的建造费用为每百米4万元.
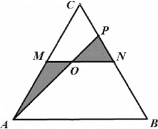
(Ⅰ)若拟修的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(Ⅱ)设![]() , 求
, 求![]() 的值,使得小路AO段与ON段的建造总费用最小.
的值,使得小路AO段与ON段的建造总费用最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
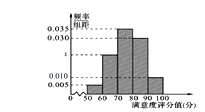
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
①![]() 在
在![]() 上是减函数;
上是减函数;
②![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
③![]() 在
在![]() 上至少有两个零点.
上至少有两个零点.
其中正确结论的序号为_________(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,左顶点为A,右顶点B在直线
,左顶点为A,右顶点B在直线![]() 上.
上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的点,直线![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 运动时,判断以
运动时,判断以![]() 为直径的圆与直线PF的位置关系,并加以证明.
为直径的圆与直线PF的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量。![]() 年,某企业连续
年,某企业连续![]() 年累计研发投入搭
年累计研发投入搭![]() 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这
亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这![]() 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
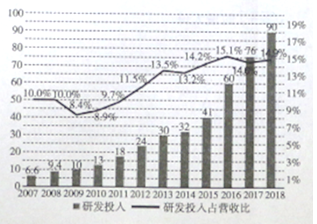
A. ![]() 年至
年至![]() 年研发投入占营收比增量相比
年研发投入占营收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研发投入增量相比
年研发投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 该企业连续![]() 年研发投入逐年增加
年研发投入逐年增加
D. 该企业来连续![]() 年来研发投入占营收比逐年增加
年来研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2(a∈R),g(x)=2ln x.
(1)讨论函数F(x)=f(x)-g(x)的单调性;
(2)若方程f(x)=g(x)在区间[![]() ,e]上有两个不等解,求a的取值范围.
,e]上有两个不等解,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com