
 ,
,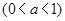
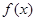 的定义域;
的定义域;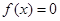 ,求
,求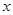 的值;
的值;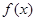 的最小值为
的最小值为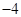 ,求
,求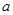 的值.
的值.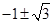 .(3)
.(3)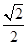 .
. 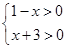 ,从而得到函数的定义域.
,从而得到函数的定义域.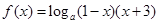 ,再由f(x)=0,得
,再由f(x)=0,得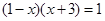 ,解此方程可得x值,要注意验证是否在定义域内.
,解此方程可得x值,要注意验证是否在定义域内.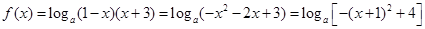 ,
,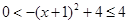 ,再根据
,再根据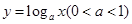 在定义域内是减函数,从而可得
在定义域内是减函数,从而可得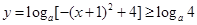 ,因而
,因而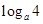 =-4,解此对数方程可得a的值.
=-4,解此对数方程可得a的值.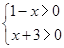 ,解之得:
,解之得: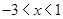 ,
,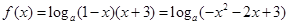 , 由
, 由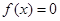 ,得
,得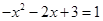 ,
,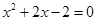 ,
,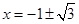 ;…………………………………………6分
;…………………………………………6分 ,
,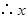 的值是
的值是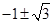 .…………………………8分
.…………………………8分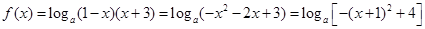 ,
,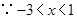
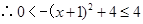 ;……………………………………………9分
;……………………………………………9分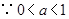 ,
,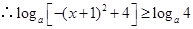 ,即
,即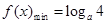 ;…………10分
;…………10分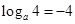 ,得
,得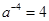 ,
,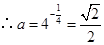 .………………………………12分
.………………………………12分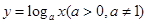 ,其定义域为
,其定义域为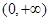 ,值域为R,当a>1时,对数函数是增函数;
,值域为R,当a>1时,对数函数是增函数;

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
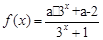 .
. 
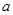 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论;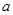 取任何实数,函数f(x)在其定义域上都是增函数;
取任何实数,函数f(x)在其定义域上都是增函数;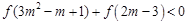 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(2,1) | B.(4,3) | C.(3,4) | D.(10,5) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
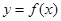 的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则
的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则 的值是
的值是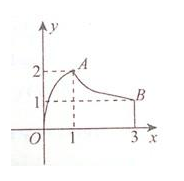
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com