分析:由于y=sinx的最小正周期2π,y=|sinx|的最小正周期为π,即对sinx加绝对值符号后周期减半,从而可判断(1)正确;
利用正弦函数的单调性可判断
y=sin(x-)在区间
[π,)上单调递增正确;将x=
代入
y=sin(2x+)不能使函数取到最大或最小值,可判断(3)错.
解答:解:∵y=sinx的最小正周期2π,y=|sinx|的最小正周期为π,即对sinx加绝对值符号后周期减半,
而y=sin(2x+
)的最小正周期为π,
∴y=|sin(2x+
)|的最小正周期
,即(1)正确;
对于(2),由于y=sin(x-
)的单调递增区间可由2kπ-
≤x-
≤2kπ+
得到,
∴2kπ+π≤x≤2kπ+2π,(k∈Z),
∴函数y=sin(x-
)的单调递增区间为[2kπ+π,2kπ+2π],(k∈Z),
令k=0,π≤x≤2π,
[π,)?[π,2π],
故函数
y=sin(x-)在区间
[π,)上单调递增,(2)正确;
将x=
代入
y=sin(2x+)得:y=sin5π=0,不是函数的最大或最小值,故(3)错误.
综上所述,正确命题的序号是(1)(2).
故答案为:(1)(2).
点评:本题考查三角函数性质,着重考查其周期性与单调性、对称轴与最值,属于中档题.



 阅读快车系列答案
阅读快车系列答案![]() )|的最小正周期是
)|的最小正周期是![]() ;(2)函数y=sin(x-
;(2)函数y=sin(x-![]() )在区间[π,
)在区间[π,![]() )上单调递增;(3)x=
)上单调递增;(3)x=![]() 是函数y=sin(2x+
是函数y=sin(2x+![]() )的图象的一条对称轴.其中正确命题的个数是
)的图象的一条对称轴.其中正确命题的个数是 的最小正周期是
的最小正周期是 ;(2)函数
;(2)函数 在区间
在区间 上单调递增;(3)
上单调递增;(3) 是函数
是函数 的图象的一条对称轴.其中正确命题的个数是( )
的图象的一条对称轴.其中正确命题的个数是( )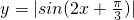 的最小正周期是
的最小正周期是 ;
; 在区间
在区间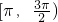 上单调递增;
上单调递增;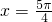 是函数
是函数 的图象的一条对称轴.
的图象的一条对称轴. 的最小正周期是
的最小正周期是 ;
; 在区间
在区间 上单调递增;
上单调递增; 是函数
是函数 的图象的一条对称轴.
的图象的一条对称轴.