
【题目】已知函数![]() .
.
(1)当![]() ,
, ![]() 时,讨论函数
时,讨论函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)当![]() 时,如果函数
时,如果函数![]() 恰有两个不同的极值点
恰有两个不同的极值点![]() ,
, ![]() ,证明:
,证明: ![]() .
.
【答案】(1)当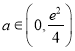 时,有
时,有![]() 个零点;当
个零点;当![]() 时,有
时,有![]() 个零点;当
个零点;当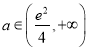 时,有
时,有![]() 个零点;(2)证明见解析.
个零点;(2)证明见解析.
【解析】试题分析:(1)研究函数![]() 的零点个数,本题直接研究函数
的零点个数,本题直接研究函数![]() 的性质,不太方便,可以进行转化,函数的零点就是方程
的性质,不太方便,可以进行转化,函数的零点就是方程![]() 的解,即
的解,即![]() 的解,而此方程解的个数可以转化为直线
的解,而此方程解的个数可以转化为直线![]() 与函数
与函数![]() 的图象交点个数,而函数
的图象交点个数,而函数![]() 是一个确定的函数,不含参数,因此求出导数
是一个确定的函数,不含参数,因此求出导数![]() 后得出它的单调性与最值后可得结论;(2)这类证明题,首先要建立极值点与参数的关系,为此求得
后得出它的单调性与最值后可得结论;(2)这类证明题,首先要建立极值点与参数的关系,为此求得![]() ,则
,则![]() 是
是![]() 的两根(由
的两根(由![]() 有两个不同的实根,首先可得出
有两个不同的实根,首先可得出![]() ),这样应有
),这样应有![]() ,
, ![]() .两式相减参数
.两式相减参数![]() 与
与![]() 的关系就出现了:
的关系就出现了: ![]() ,要证的题设不等式就变为要证
,要证的题设不等式就变为要证![]() ,
, ![]() (两边除以
(两边除以![]() 可得),即证
可得),即证![]() ,
,
即证![]() ,于是只要设
,于是只要设![]() ,
, ![]() .即证不等式
.即证不等式![]() ,当
,当![]() 时恒成立.这可由利用导数的知识证明.
时恒成立.这可由利用导数的知识证明.
试题解析:(1)当![]() ,
, ![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的零点的个数即方程
上的零点的个数即方程![]() 根的个数.
根的个数.
由![]() ,
,
令 ,
,
则![]() 在
在![]() 上单调递减,这时
上单调递减,这时![]() ;
;
![]() 在
在![]() 上单调递增,这时
上单调递增,这时![]() .
.
所以![]() 是
是![]() 的极小值即最小值,即
的极小值即最小值,即![]()
所以函数![]() 在区间
在区间![]() 上零点的个数,讨论如下:
上零点的个数,讨论如下:
当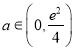 时,有
时,有![]() 个零点;
个零点;
当![]() 时,有
时,有![]() 个零点;
个零点;
当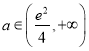 时,有
时,有![]() 个零点.
个零点.
(2)由已知![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]() 是函数
是函数![]() 的两个不同极值点(不妨设
的两个不同极值点(不妨设![]() ),
),
![]()
![]() (若
(若![]() 时,
时, ![]() ,即
,即![]() 是
是![]() 上的增函数,与已知矛盾),
上的增函数,与已知矛盾),
且![]() ,
, ![]() .
.
![]()
![]() ,
, ![]() .
.
两式相减得: ![]() ,
,
于是要证明![]() ,即证明
,即证明![]() ,两边同除以
,两边同除以![]() ,即
,即
证![]() ,即证
,即证![]() ,
,
即证![]() ,
,
令![]() ,
, ![]() .即证不等式
.即证不等式![]() ,当
,当![]() 时恒成立.
时恒成立.
设![]() ,
, ![]()
![]()
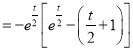 .
.
设![]() ,
, ![]()
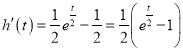 ,当
,当![]() ,
, ![]() ,
,
![]() 单调递减,所以
单调递减,所以![]() ,即
,即![]() ,
, ![]()
![]() ,
,
![]()
![]() 在
在![]() 时是减函数.
时是减函数. ![]()
![]() 在
在![]() 处取得极小值
处取得极小值![]() .
.
![]()
![]() ,得证.
,得证. ![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|2a≤x<a+3},B={x|x<﹣1或x>5}.
(1)若a=﹣1,求A∪B,(RA)∩B.
(2)若A∩B=,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(1)的前提下,记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列及生产1件芯片甲和1件芯片乙所得总利润的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
(α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为 ![]() .
.
(1)求C的普通方程和l的倾斜角;
(2)设点P(0,2),l和C交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
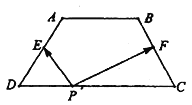
【题目】如图,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和![]() 分别为
分别为![]() 与
与![]() 的中点,对于常数
的中点,对于常数![]() ,在梯形
,在梯形![]() 的四条边上恰好有8个不同的点
的四条边上恰好有8个不同的点![]() ,使得
,使得![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com