【题目】稠环芳香烃化合物中有不少是致癌物质，比如学生钟爱的快餐油炸食品中会产生苯并芘，它是由一个苯环和一个芘分子结合而成的稠环芳香烃类化合物，长期食用会致癌.下面是一组稠环芳香烃的结构简式和分子式：
名称 | 萘 | 蒽 | 并四苯 | … | 并n苯 |
结构简式 |
|
|
| … | … |
分子式 |
|
|
| … | … |
由此推断并十苯的分子式为________.
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，直线
的参数方程为
（
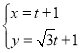为参数），以原点为极点，
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程为
．
（1）写出直线的极坐标方程与曲线的直角坐标方程；
（2）已知与直线平行的直线
过点
，且与曲线交于
两点，试求
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
.
（1）求
的单调区间；
（2）设曲线
与
轴正半轴的交点为
，曲线在点处的切线方程为
，求证：对于任意的实数，都有
；
（3）若方程
为实数）有两个实数根
，
，且
，求证：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某种新型病毒的传染能力很强，给人们生产和生活带来很大的影响，所以创新研发疫苗成了当务之急.为此，某药企加大了研发投入，市场上这种新型冠状病毒的疫苗
的研发费用
（百万元）和销量
（万盒）的统计数据如下：
研发费用 | 2 | 3 | 6 | 10 | 13 | 14 |
销量 | 1 | 1 | 2 | 2.5 | 4 | 4.5 |
（1）根据上表中的数据，建立关于的线性回归方程
（用分数表示）；
（2）根据所求的回归方程，估计当研发费用为1600万元时，销售量为多少？
参考公式：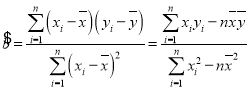
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂生产了一批零件，从中随机抽取100个作为样本，测出它们的长度（单位：厘米），按数据分成
，
，
，
，
5组，得到如图所示的频率分布直方图．以这100个零件的长度在各组的频率代替整批零件长度在该组的概率．
（1）估计该工厂生产的这批零件长度的平均值（同一组中的每个数据用该组区间的中点值代替）；
（2）若用分层抽样的方式从第1组和第5组中抽取5个零件，再从这5个零件中随机抽取2个，求抽取的零件中恰有1个是第1组的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知椭圆
短轴的两个顶点与右焦点的连线构成等边三角形，两准线之间的距离为
.
（1）求椭圆
的标准方程；
（2）直线
与椭圆交于
，
两点，设直线
，
的斜率分别为
，
.已知
.
①求
的值；
②当
的面积最大时，求直线
的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，圆
的方程为
，以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，直线
的极坐标方程为
．
（1）求圆的极坐标方程与直线的直角坐标方程；
（2）设直线与圆相交于
，
两点，求圆在，处两条切线的交点坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在极坐标系中，点P的坐标是
，曲线C的方程为
.以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，斜率为
的直线l经过点P.
（1）写出直线l的参数方程和曲线C的直角坐标方程；
（2）若直线l和曲线C相交于两点A，B，求
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
