
【题目】设n为正整数,集合A=![]() .对于集合A中的任意元素
.对于集合A中的任意元素![]() 和
和![]() ,记
,记
M(![]() )=
)=![]() .
.
(Ⅰ)当n=3时,若![]() ,
, ![]() ,求M(
,求M(![]() )和M(
)和M(![]() )的值;
)的值;
(Ⅱ)当n=4时,设B是A的子集,且满足:对于B中的任意元素![]() ,当
,当![]() 相同时,M(
相同时,M(![]() )是奇数;当
)是奇数;当![]() 不同时,M(
不同时,M(![]() )是偶数.求集合B中元素个数的最大值;
)是偶数.求集合B中元素个数的最大值;
(Ⅲ)给定不小于2的n,设B是A的子集,且满足:对于B中的任意两个不同的元素![]() ,
,
M(![]() )=0.写出一个集合B,使其元素个数最多,并说明理由.
)=0.写出一个集合B,使其元素个数最多,并说明理由.
【答案】(1) M(α,β)=1
(2) 最大值为4
(3)答案见解析
【解析】分析:(1)根据定义对应代入可得M(![]() )和M(
)和M(![]() )的值;(2)先根据定义得M(α,α)= x1+x2+x3+x4.再根据x1,x 2,x3,x4∈{0,1},且x1+x2+x3+x4为奇数,确定x1,x 2,x3,x4中1的个数为1或3.可得B元素最多为8个,再根据当
)的值;(2)先根据定义得M(α,α)= x1+x2+x3+x4.再根据x1,x 2,x3,x4∈{0,1},且x1+x2+x3+x4为奇数,确定x1,x 2,x3,x4中1的个数为1或3.可得B元素最多为8个,再根据当![]() 不同时,M(
不同时,M(![]() )是偶数代入验证,这8个不能同时取得,最多四个,最后取一个四元集合满足条件,即得B中元素个数的最大值;(3)因为M(
)是偶数代入验证,这8个不能同时取得,最多四个,最后取一个四元集合满足条件,即得B中元素个数的最大值;(3)因为M(![]() )=0,所以
)=0,所以![]() 不能同时取1,所以取
不能同时取1,所以取![]() 共n+1个元素,再利用A的一个拆分说明B中元素最多n+1个元素,即得结果.
共n+1个元素,再利用A的一个拆分说明B中元素最多n+1个元素,即得结果.
详解:解:(Ⅰ)因为α=(1,1,0),β=(0,1,1),所以
M(α,α)= ![]() [(1+1|11|)+(1+1|11|)+(0+0|00|)]=2,
[(1+1|11|)+(1+1|11|)+(0+0|00|)]=2,
M(α,β)=![]() [(1+0–|10|)+(1+1–|1–1|)+(0+1–|0–1|)]=1.
[(1+0–|10|)+(1+1–|1–1|)+(0+1–|0–1|)]=1.
(Ⅱ)设α=(x1,x 2,x3,x4)∈B,则M(α,α)= x1+x2+x3+x4.
由题意知x1,x 2,x3,x4∈{0,1},且M(α,α)为奇数,
所以x1,x 2,x3,x4中1的个数为1或3.
所以B![]() {(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}.
{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}.
将上述集合中的元素分成如下四组:
(1,0,0,0),(1,1,1,0);(0,1,0,0),(1,1,0,1);(0,0,1,0),(1,0,1,1);(0,0,0,1),(0,1,1,1).
经验证,对于每组中两个元素α,β,均有M(α,β)=1.
所以每组中的两个元素不可能同时是集合B的元素.
所以集合B中元素的个数不超过4.
又集合{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}满足条件,
所以集合B中元素个数的最大值为4.
(Ⅲ)设Sk=( x1,x 2,…,xn)|( x1,x 2,…,xn)∈A,xk=1,x1=x2=…=xk–1=0)(k=1,2,…,n),
Sn+1={( x1,x 2,…,xn)| x1=x2=…=xn=0},
则A=S1∪S1∪…∪Sn+1.
对于Sk(k=1,2,…,n–1)中的不同元素α,β,经验证,M(α,β)≥1.
所以Sk(k=1,2 ,…,n–1)中的两个元素不可能同时是集合B的元素.
所以B中元素的个数不超过n+1.
取ek=( x1,x 2,…,xn)∈Sk且xk+1=…=xn=0(k=1,2,…,n–1).
令B=(e1,e2,…,en–1)∪Sn∪Sn+1,则集合B的元素个数为n+1,且满足条件.
故B是一个满足条件且元素个数最多的集合.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:阳马指底面为矩形,一侧棱垂直于底面的四棱锥,堑堵指底面是直角三角形,且侧棱垂直于底面的三棱柱.
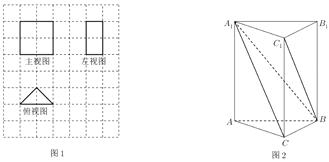
(1)某堑堵的三视图,如图1,网格中的每个小正方形的边长为1,求该堑堵的体积;
(2)在堑堵![]() 中,如图2,
中,如图2,![]() ,若
,若![]() ,当阳马
,当阳马![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 是它的上顶点,点
是它的上顶点,点![]() 各不相同且均在椭圆上.
各不相同且均在椭圆上.
(1)若![]() 恰为椭圆长轴的两个端点,求
恰为椭圆长轴的两个端点,求![]() 的面积;
的面积;
(2)若![]() ,求证:直线
,求证:直线![]() 过一定点;
过一定点;
(3)若![]() ,
,![]() 的外接圆半径为
的外接圆半径为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若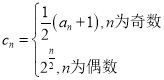
![]() ,从数列
,从数列![]() 中抽出部分项(奇数项与偶数项均不少于两项),将抽出的项按照某一顺序排列后构成等差数列.当等差数列的项数最大时,求所有满足条件的等差数列.
中抽出部分项(奇数项与偶数项均不少于两项),将抽出的项按照某一顺序排列后构成等差数列.当等差数列的项数最大时,求所有满足条件的等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com