
分析 (1)由△ABC的面积为3,可得bc=$\frac{6}{sinθ}$.由2$\sqrt{3}$≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6,可得$2\sqrt{3}≤$bccosθ≤6,θ∈$(0,\frac{π}{2})$.化为1≤tanθ≤$\sqrt{3}$,即可得出.
(2)函数f(θ)=2sin2($\frac{π}{4}$+θ)-cos2θ=$\sqrt{2}sin(2θ-\frac{π}{4})$+1,利用θ∈$[\frac{π}{4},\frac{π}{3}]$.可得$(2θ-\frac{π}{4})$∈$[\frac{π}{4},\frac{5π}{12}]$,即可得出.
解答 解:(1)∵△ABC的面积为3,∴$\frac{1}{2}bcsinθ$=3,∴bc=$\frac{6}{sinθ}$.
∵2$\sqrt{3}$≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6,
∴$2\sqrt{3}≤$bccosθ≤6,θ∈$(0,\frac{π}{2})$.
∴$2\sqrt{3}$≤6×$\frac{cosθ}{sinθ}$≤6,
∴1≤tanθ≤$\sqrt{3}$,
∴θ∈$[\frac{π}{4},\frac{π}{3}]$.
(2)函数f(θ)=2sin2($\frac{π}{4}$+θ)-cos2θ
=$1-cos(\frac{π}{2}+2θ)$-cos2θ
=1+sin2θ-cos2θ
=$\sqrt{2}sin(2θ-\frac{π}{4})$+1,
∵θ∈$[\frac{π}{4},\frac{π}{3}]$.
∴$(2θ-\frac{π}{4})$∈$[\frac{π}{4},\frac{5π}{12}]$,
当$2θ-\frac{π}{4}$=$\frac{π}{4}$,即$θ=\frac{π}{4}$时,$sin(2θ-\frac{π}{4})$=$\frac{\sqrt{2}}{2}$,此时f(θ)取得最小值2.
点评 本题考查了向量数量积运算性质、三角形面积计算公式、倍角公式、三角函数的单调性、和差公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD与正方形ABEF边长均为1,且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动,若CM=BN=α(0<α<$\sqrt{2}$)
如图,正方形ABCD与正方形ABEF边长均为1,且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动,若CM=BN=α(0<α<$\sqrt{2}$)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
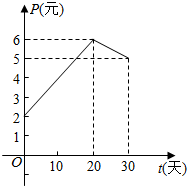 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).
某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com