
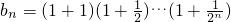 ,
,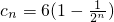 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,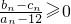 .
. ≥qn①
≥qn① (n∈N*).
(n∈N*). ,与①矛盾,故假设不成立.(9分)
,与①矛盾,故假设不成立.(9分)
 ,
,
 ,…,猜想:bn≤cn.
,…,猜想:bn≤cn.
 =
=
 =
= =
=
 =ck+1
=ck+1 .
.
 .
. ≤2cn-1=
≤2cn-1= <12.
<12. .
. ,an-12<0.
,an-12<0.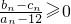 .(14分)
.(14分) ≥qn①,因为q>1,所以?n0∈N*,使得当n≥n0时,qn>2,从而
≥qn①,因为q>1,所以?n0∈N*,使得当n≥n0时,qn>2,从而 >2,与
>2,与 ≤2矛盾,于是可判断数列{an}不能为等比数列;
≤2矛盾,于是可判断数列{an}不能为等比数列;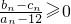 的分子部分,可根据b1=c1=3,结合已知条件,求得b2,c2;b3,c3通过比较两者的大小,猜想bn≤cn.然后用数学归纳法予以证明;对于其分母,可结合条件证明an<12,从而是问题得到解决.
的分子部分,可根据b1=c1=3,结合已知条件,求得b2,c2;b3,c3通过比较两者的大小,猜想bn≤cn.然后用数学归纳法予以证明;对于其分母,可结合条件证明an<12,从而是问题得到解决.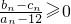 需分别从分子与分母两处着手,用数学归纳法证明bn≤cn,用放缩法证明an-12<0,属于难题.
需分别从分子与分母两处着手,用数学归纳法证明bn≤cn,用放缩法证明an-12<0,属于难题. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 1 |
| an |
| 4n |
| n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2n |
| bn-cn |
| an-12 |
查看答案和解析>>
科目:高中数学 来源:北京模拟题 题型:解答题
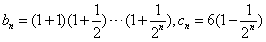 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,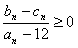 。
。 查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市海淀区北师特学校高三(上)第四次月考数学试卷(理科)(解析版) 题型:解答题
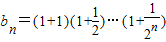 ,
,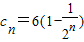 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,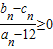 .
.查看答案和解析>>
科目:高中数学 来源:2011年北京市东城区高考数学二模试卷(理科)(解析版) 题型:解答题
 ,
, ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,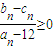 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com