


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源:不详 题型:解答题
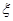 ,求
,求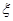 的数学期望
的数学期望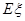 (即均值).
(即均值).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
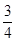 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是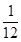 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是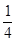 .(Ⅰ)求乙、丙两人各自回答对这道题的概率;(Ⅱ)用
.(Ⅰ)求乙、丙两人各自回答对这道题的概率;(Ⅱ)用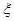 表示回答对该题的人数,求
表示回答对该题的人数,求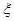 的分布列和数学期望E
的分布列和数学期望E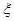 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
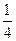 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。
;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。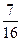 ,求走公路②堵的概率;
,求走公路②堵的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.0324 | B.0.0434 | C.0.0528 | D.0.0562 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com