
【题目】某地上年度电价为![]() 元,年用电量为
元,年用电量为![]() 亿千瓦时.本年度计划将电价调至
亿千瓦时.本年度计划将电价调至![]() 之间,经测算,若电价调至
之间,经测算,若电价调至![]() 元,则本年度新增用电量
元,则本年度新增用电量![]() (亿千瓦时)与
(亿千瓦时)与![]() 元成反比例.又当
元成反比例.又当![]() 时,
时,![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为![]() 元,则电价调至多少时,本年度电力部门的收益将比上年增加
元,则电价调至多少时,本年度电力部门的收益将比上年增加![]() ?[收益=用电量×(实际电价-成本价)]
?[收益=用电量×(实际电价-成本价)]
科目:高中数学 来源: 题型:
【题目】从某自动包装机包袋的食盐中,随机抽取![]() 袋作为样本,按各袋的质量(单位:
袋作为样本,按各袋的质量(单位: ![]() )分成四组,
)分成四组, ![]() ,相应的样本频率分布直方图如图所示.
,相应的样本频率分布直方图如图所示.
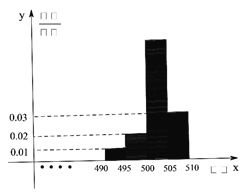
(Ⅰ)估计样本的中位数是多少?落入![]() 的频数是多少?
的频数是多少?
(Ⅱ)现从这台自动包装机包袋的大批量食盐中,随机抽取![]() 袋,记
袋,记![]() 表示食盐质量属于
表示食盐质量属于![]() 的袋数,依样本估计总体的统计思想,求
的袋数,依样本估计总体的统计思想,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆O:x2+y2=8内有一点P(﹣1,2),AB为过点P且倾斜角为α的弦,
(1)当α=135°时,求AB的长;
(2)当弦AB被点P平分时,写出直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心半径为
为圆心半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围;
的取值范围;
(3)设![]() 是圆
是圆![]() 上的两个动点,点
上的两个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,如果直线
,如果直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 和
和![]() ,问
,问![]() 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() 恰好为线段
恰好为线段![]() 的三等分点,求直线
的三等分点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
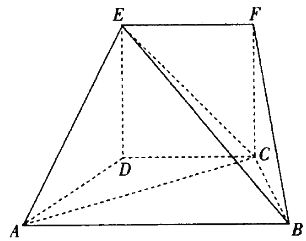
![]() 求BE与平面EAC所成角的正弦值;
求BE与平面EAC所成角的正弦值;
![]() 线段BE上是否存在点M,使平面
线段BE上是否存在点M,使平面![]() 平面DFM?若存在,求
平面DFM?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3.

(1)设G,H分别为PB,AC的中点,求证:GH//平面PAD;
(2)求证:![]() ⊥平面PCD;
⊥平面PCD;
(3)求直线AD与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 为焦点是
为焦点是![]() 的抛物线上一点,
的抛物线上一点, ![]() 为直线
为直线![]() 上任一点,
上任一点, ![]() 分别为椭圆
分别为椭圆![]() 的上,下顶点,且
的上,下顶点,且![]() 三点的连线可以构成三角形.
三点的连线可以构成三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点分别交于点
的另一交点分别交于点![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com