
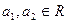 且
且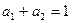 ,求证
,求证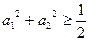
 函数
函数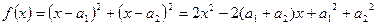 因为对一切
因为对一切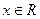 ,恒有
,恒有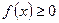 ,所以
,所以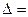 4-8
4-8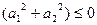 ,从而
,从而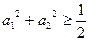
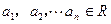 ,且
,且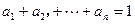 ,请写出上述结论的推广式;
,请写出上述结论的推广式;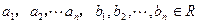 ,求证
,求证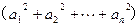
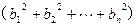
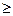
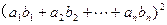 .[
.[科目:高中数学 来源:不详 题型:填空题
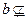 平面
平面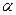 ,直线
,直线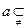 平面
平面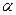 ,直线
,直线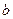 ∥平面
∥平面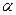 ,则直线
,则直线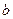 ∥直线
∥直线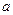 ”的结论显然是错误的,这是因为
”的结论显然是错误的,这是因为 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
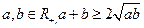 ------------- 大前提
------------- 大前提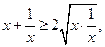 -------------- 小前提
-------------- 小前提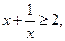 --
-- -------
------- ------- 结论
------- 结论 过程中的错误为
过程中的错误为 ( )
( )| A.大前提 | B.小前提 | C.结论 | D.无错误 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,斜边长为
,斜边长为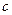 ,斜边上的高为
,斜边上的高为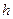 ,则有
,则有 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论: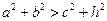 ;②
;②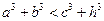 ;③
;③ 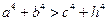 ;④
;④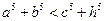 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.正方形的对角线相等 | B.矩形的对角线相等 | C.正方形是矩形 | D.其 他 他 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 .设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥 ,若用
,若用 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,你类比得到的结论是 .
表示截面面积,你类比得到的结论是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com