
如图,直线y=kx+b与椭圆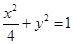 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.
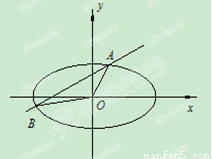
(1)求在k=0,0<b<1的条件下,S的最大值;
(2)当|AB|=2,S=1时,求直线AB的方程.
(1)1;(2)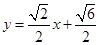 或
或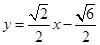 或
或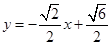 或
或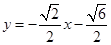 .
.
【解析】
试题分析:(1)直线与椭圆(圆锥曲线)相交和直线与圆相交的问题有区别,直线与圆相交可以利用圆的一些性质,用几何方法解决问题,而直线与椭圆(圆锥曲线)相交只能用解析法解题。这里直接求出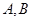 两点有坐标(用
两点有坐标(用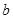 表示),求出三角形的面积,相当于把
表示),求出三角形的面积,相当于把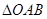 的面积
的面积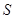 表示成了
表示成了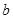 的函数,然后用不等式的知识或函数知识求出最大值。(2)同样把直线方程
的函数,然后用不等式的知识或函数知识求出最大值。(2)同样把直线方程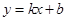 与椭圆方程
与椭圆方程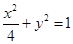 联立,消去
联立,消去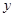 ,得出关于
,得出关于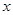 的二次方程,
的二次方程,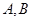 两点的横坐标
两点的横坐标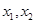 就是这个方程的两解,故必须满足
就是这个方程的两解,故必须满足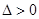 ,而线段
,而线段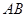 的长
的长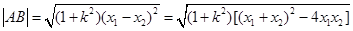 ,再求出原点到直线
,再求出原点到直线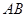 的距离,利用面积
的距离,利用面积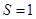 ,列出关于
,列出关于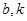 的方程组,解出
的方程组,解出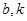 ,即直线
,即直线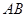 的方程。
的方程。
试题解析:解:设点A的坐标为(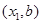 ,点B的坐标为
,点B的坐标为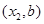 ,
,
由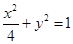 ,解得
,解得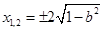
所以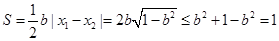
当且仅当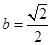 时,.S取到最大值1.
时,.S取到最大值1.
(Ⅱ)解:由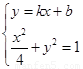 得
得
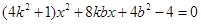
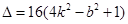 ①
①
|AB|=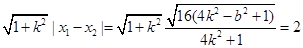 ②
②
又因为O到AB的距离 所以
所以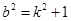 ③
③
③代入②并整理,得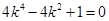
解得,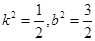 ,代入①式检验,△>0
,代入①式检验,△>0
故直线AB的方程是
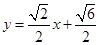 或
或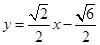 或
或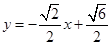 或
或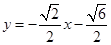 .
.
考点:直线与椭圆相交,弦长公式。


科目:高中数学 来源: 题型:
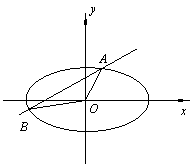 如图,直线y=kx+b与椭圆
如图,直线y=kx+b与椭圆![]() 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.
(I)求在k=0,0<b<1的条件下,S的最大值;
(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
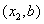
(I)求在k=0,0<b<1的条件下,S的最大值;
(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题14分)如图,直线y=kx+b与椭圆![]() 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.
(I)求在k=0,0<b<1的条件下,S的最大值;
(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题14分)如图,直线y=kx+b与椭圆![]() 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.
(I)求在k=0,0<b<1的条件下,S的最大值;
(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com