
【题目】一旅游区有两个新建项目![]() 、
、![]() .
.![]() 项目的一期投资额
项目的一期投资额![]() 与利润
与利润![]() 近似满足
近似满足![]() .
.![]() 项目的一期投资额
项目的一期投资额![]() 与利润
与利润![]() 的关系如散点图所示,其中
的关系如散点图所示,其中![]()
![]() ,
,![]() ,
,![]() .一商家欲向这两个项目一期随机投资,其中投资
.一商家欲向这两个项目一期随机投资,其中投资![]() 项目不超过10(本题未注明金额单位的,单位均为百万元).投资
项目不超过10(本题未注明金额单位的,单位均为百万元).投资![]() 、
、![]() 相互独立.
相互独立.
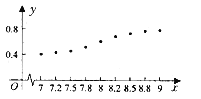
(1)用最小二乘法求![]() 与
与![]() 的回归直线方程;
的回归直线方程;
(2)商家投资![]() 项目的概率是0.4,投资
项目的概率是0.4,投资![]() 项目的概率是0.6.设商家这次投资获得的利润最大值为
项目的概率是0.6.设商家这次投资获得的利润最大值为![]() ,利用(1)的结果,求
,利用(1)的结果,求![]() .
.
附参考公式: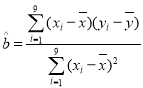 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早、晚读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成下表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为30%,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: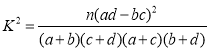 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选![]() 名患者随机分成两组,每组各
名患者随机分成两组,每组各![]() 名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标
名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标![]() 和
和![]() 的数据,并制成如图,其中“
的数据,并制成如图,其中“![]() ”表示服药者,“
”表示服药者,“![]() ”表示未服药者.
”表示未服药者.
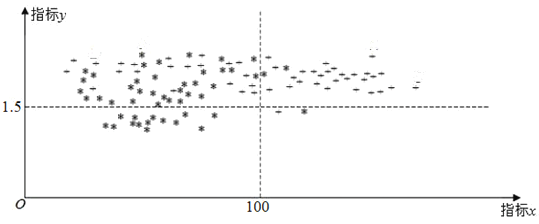
下列说法中,错误的是( )
A.服药组的指标![]() 的均值和方差比未服药组的都低
的均值和方差比未服药组的都低
B.未服药组的指标![]() 的均值和方差比服药组的都高
的均值和方差比服药组的都高
C.以统计的频率作为概率,患者服药一段时间后指标![]() 低于
低于![]() 的概率约为
的概率约为![]()
D.这种疾病的患者的生理指标![]() 基本都大于
基本都大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①![]() 使得
使得![]() 成立;②
成立;②![]() ,都有
,都有![]() 成立,是
成立,是![]() 在区间D上单调递增的充要条件;③只要函数有零点,我们就可以用二分法求出零点的近似值;④过点
在区间D上单调递增的充要条件;③只要函数有零点,我们就可以用二分法求出零点的近似值;④过点![]() 作直线,使它与抛物线
作直线,使它与抛物线![]() 仅有一个公共点,这样的直线有2条;正确的个数是( )
仅有一个公共点,这样的直线有2条;正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由![]() 个人依次出场解密,每人限定时间是
个人依次出场解密,每人限定时间是![]() 分钟内,否则派下一个人.
分钟内,否则派下一个人.![]() 个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲
个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲![]() 次的测试记录,绘制了如下的频率分布直方图.
次的测试记录,绘制了如下的频率分布直方图.
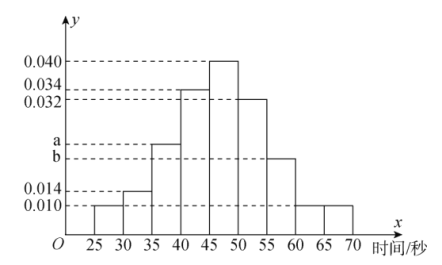
(1)若甲解密成功所需时间的中位数为![]() ,求
,求![]() 、
、![]() 的值,并求出甲在
的值,并求出甲在![]() 分钟内解密成功的频率;
分钟内解密成功的频率;
(2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为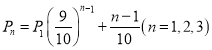 ,其中
,其中![]() 表示第
表示第![]() 个出场选手解密成功的概率,并且
个出场选手解密成功的概率,并且![]() 定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
①求该团队挑战成功的概率;
②该团队以![]() 从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目
从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com