
【题目】已知函数f(x)=axex,g(x)=x2+2x+b,若曲线y=f(x)与曲线y=g(x)都过点P(1,c).且在点P处有相同的切线l.
(Ⅰ)求切线l的方程;
(Ⅱ)若关于x的不等式k[ef(x)]≥g(x)对任意x∈[﹣1,+∞)恒成立,求实数k的取值范围.
【答案】(Ⅰ)4x﹣y﹣2=0;(Ⅱ)![]() k≤e
k≤e
【解析】
(I)根据切点和斜率列方程,解方程组求得![]() 的值,进而求得切线方程.
的值,进而求得切线方程.
(II)构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调性,对
的单调性,对![]() 进行分类讨论,结合
进行分类讨论,结合![]() 恒成立,由此求得
恒成立,由此求得![]() 的取值范围.
的取值范围.
(Ⅰ)∵f′(x)=aex(x+1),g′(x)=2x+2,由已知可得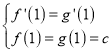 ,
,
即![]() ,解得a
,解得a![]() ,b=﹣1,c=2,∴切线的斜率g′(1)=4,
,b=﹣1,c=2,∴切线的斜率g′(1)=4,
∴切线l的方程为y﹣2=4(x﹣1),即4x﹣y﹣2=0,
(Ⅱ)由(Ⅰ)可得f(x)=2xex﹣1,g(x)=x2+2x﹣1,设h(x)=k[ef(x)]﹣g(x)=2kxex﹣(x2+2x﹣1),
即h(x)≥0,对任意x∈[﹣1,+∞)恒成立,从而h(x)min≥0,
∴h′(x)=2k(x+1)ex﹣2(x+1)=2(x+1)(kex﹣1),
①当k≤0时,h′(x)≤0,h(x)在[﹣1,+∞)上单调递减,又h(1)=2ke﹣2<0,显然h(x)≥0不恒成立,
②当k>0时,h′(x)=0,解得x1=﹣1,x2=﹣lnk,
(i)当﹣lnk<﹣1时,即k>e时,h′(x)≥0,h(x)单调递增,
又h(x)min=h(﹣1)![]() 2
2![]() 0,显然h(x)≥0不恒成立,
0,显然h(x)≥0不恒成立,
(ii)当﹣lnk=﹣1时,即k=e时,h′(x)>0,h(x)单调递增,
∴h(x)min=h(﹣1)![]() 2
2![]() 0,即h(x)≥0恒成立,
0,即h(x)≥0恒成立,
(iii)当﹣lnk>﹣1时,即0<k<e时,
当x∈[﹣1,﹣lnk)时,h′(x)<0,h(x)单调递减,当x∈(﹣lnk,+∞)时,h′(x)>0,h(x)单调递增,
∴h(x)min=h(﹣lnk)=-2lnk﹣(ln2k﹣2lnk﹣1)=1﹣ln2k≥0,解得![]() k≤e,∴
k≤e,∴![]() k<e,
k<e,
综上所述得:![]() k≤e.
k≤e.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为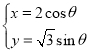 (
(![]() 为参数),若以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线
为参数),若以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点P的坐标为![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 交于C,D两点,求
交于C,D两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推进长三角一体化战略,长三角区域内5个大型企业举办了一次协作论坛.在这5个企业董事长A,B,C,D,E集体会晤之前,除B与E,D与E不单独会晤外,其他企业董事长两两之间都要单独会晤.现安排他们在正式会晤的前两天的上午、下午单独会晤(每人每个半天最多只进行一次会晤),那么安排他们单独会晤的不同方法共有( )
A.48种B.36种C.24种D.8种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”.整个图形是一个圆形.其中黑色阴影区域在y轴右侧部分的边界为一个半圆,给出以下命题:
①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]()
②当![]() 时,直线y=ax+2a与白色部分有公共点;
时,直线y=ax+2a与白色部分有公共点;
③黑色阴影部分(包括黑白交界处)中一点(x,y),则x+y的最大值为2;
④设点P(﹣2,b),点Q在此太极图上,使得∠OPQ=45°,b的范围是[﹣2,2].
其中所有正确结论的序号是( )
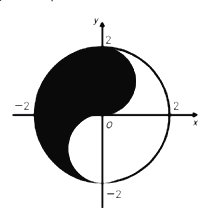
A.①④B.①③C.②④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,SD=CD=SC=2AB=2BC,平面ABCD⊥底面SDC,AB∥CD,∠ABC=90°,E是SD中点.
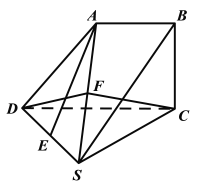
(1)证明:直线AE//平面SBC;
(2)点F为线段AS的中点,求二面角F﹣CD﹣S的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杭州西溪国家湿地公园是以水为主题的公园,以湿地良好生态环境和多样化湿地景观资源为基础的生态型主题公园.欲在该公园内搭建一个平面凸四边形![]() 的休闲观光及科普宣教的平台,如图所示,其中
的休闲观光及科普宣教的平台,如图所示,其中![]() 百米,
百米,![]() 百米,
百米,![]() 为正三角形.建成后
为正三角形.建成后![]() 将作为人们旅游观光休闲娱乐的区域,
将作为人们旅游观光休闲娱乐的区域,![]() 将作为科普宣教湿地功能利用弘扬湿地文化的区域.
将作为科普宣教湿地功能利用弘扬湿地文化的区域.
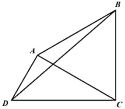
(1)当![]() 时,求旅游观光休闲娱乐的区域
时,求旅游观光休闲娱乐的区域![]() 的面积;
的面积;
(2)求旅游观光休闲娱乐的区域![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在1,2,3,4,5,6这六个数字所组成的允许有重复数字的三位数中,各个数位上的数字之和为9的三位数共有( )
A.16个B.18个C.24个D.25个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为60°,求平面
所成角为60°,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com