
【题目】已知函数![]() .
.
(1)当![]() 且
且![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 的两个极值点分别为
的两个极值点分别为![]() 、
、![]() ,证明
,证明![]() .
.
【答案】(1)![]() 的单调递增区间为
的单调递增区间为![]() ,;无单调递减区间;(2)证明见解析.
,;无单调递减区间;(2)证明见解析.
【解析】
(1)求得![]() ,分类讨论,即可求解
,分类讨论,即可求解![]() 的单调区间,得到答案;
的单调区间,得到答案;
(2)根据![]() 是函数
是函数![]() 的两个零点,设
的两个零点,设![]() 是方程
是方程![]() 的两个实数解,再根据二次函数的性质函数
的两个实数解,再根据二次函数的性质函数![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值,进而得到
处取得极小值,进而得到![]() ,代入得
,代入得 ,令
,令![]() ,则
,则![]() ,得到
,得到![]() ,设
,设![]() ,利用导数求得函数的单调性与最值,即可求解.
,利用导数求得函数的单调性与最值,即可求解.
(1)由题意,当![]() 时,
时,![]() ,
,![]() ,
,
①当![]() 时,
时,![]() 恒成立,所以函数
恒成立,所以函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
②当![]() 时,记
时,记![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,∴
,∴![]() 单调递减,且
单调递减,且![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递增,且
单调递增,且![]() ,
,
所以当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
综上所述,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ;无单调递减区间.
;无单调递减区间.
(2)由![]() ,
,
![]() ,
,
![]() 是函数
是函数![]() 的两个零点,
的两个零点,
![]() 是方程
是方程![]() 的两个实数解,
的两个实数解,
由![]() ,且
,且![]() ,得
,得![]() ,则有
,则有![]() ,
,
不妨设![]() ,
,![]()
又![]() ,即得
,即得![]() ,
,
![]() ,
,![]() ,
,
即得![]() ,从而得到
,从而得到![]() ,
,
![]() ,且
,且![]() ,
,
![]() 由二次函数的图象及性质知函数
由二次函数的图象及性质知函数![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值.
处取得极小值.
![]()


 , (*)
, (*)
又![]() 为方程
为方程![]() 的根,
的根,![]() ,
,
代人(*)式得 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
从而有![]() ,
,![]() .
.
![]() ,即
,即![]() 得证.
得证.


科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著.下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图.下列描述错误的是( )
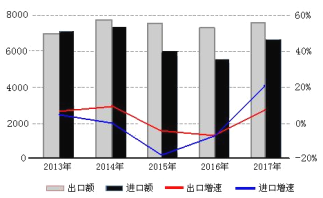
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: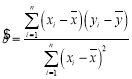 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为![]() 的数列
的数列![]() 各项均为正数,且
各项均为正数,且![]() ,
,![]() .
.
(1)若数列![]() 的通项
的通项![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() ;
;
(2)若数列![]() 的通项
的通项![]() 满足
满足 ,前n项和为
,前n项和为![]() ,当数列
,当数列![]() 是等差数列时,对任意的
是等差数列时,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 构成的集合.
构成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市场上有一种新型的强力洗衣粉,特点是去污速度快,已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中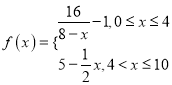 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
(1)若只投放一次4个单位的洗衣液,则有效去污时间可能达几分钟?
(2)若先投放2个单位的洗衣液,6分钟后投放![]() 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: ![]() 取
取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
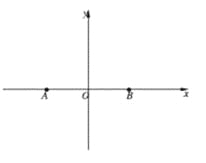
【题目】某海域有![]() 两个岛屿,
两个岛屿,![]() 岛在
岛在![]() 岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线![]() ,曾有渔船在距
,曾有渔船在距![]() 岛、
岛、![]() 岛距离和为8海里处发出过鱼群。以
岛距离和为8海里处发出过鱼群。以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 的垂直平分线为
的垂直平分线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)某日,研究人员在![]() 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),![]() 两岛收到鱼群在
两岛收到鱼群在![]() 处反射信号的时间比为
处反射信号的时间比为![]() ,问你能否确定
,问你能否确定![]() 处的位置(即点
处的位置(即点![]() 的坐标)?
的坐标)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村扶贫. 此帮扶单位为了了解某地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:
贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名贫困户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若贫困户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.运用样本估计总体的思想,现从(1)中抽到的10个样本的满意度为“
级”.运用样本估计总体的思想,现从(1)中抽到的10个样本的满意度为“![]() 级”贫困户中随机地抽取2户,求所抽到2户的满意度均评分均“超过80”的概率.
级”贫困户中随机地抽取2户,求所抽到2户的满意度均评分均“超过80”的概率.
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
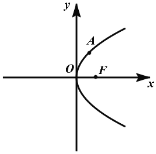
【题目】如图,在平面直角坐标系![]() 中,己知抛物线
中,己知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的一点,点
上的一点,点![]() 的坐标为
的坐标为![]()
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)弦![]() 经过点
经过点![]() ,过弦
,过弦![]() 上一点
上一点![]() 作直线
作直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,求证:“直线
,求证:“直线![]() 与抛物线相切”的一个充要条件是“
与抛物线相切”的一个充要条件是“![]() 为弦
为弦![]() 的中点”.
的中点”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com