①②③④
分析:①由f(x+1)=-f(x),可得f[(x+1)+1]=f(x),由周期函数的定义可以判断①的正误;
②利用

是偶函数,采用换元法,结合周期性可判断其奇偶性;
③设出y=f(x)上任意一点P(x
0,y
0)关于(1,0)的对称点为P′(2-x
0,-y
0),由曲线关于点对称的定义去判断正误;
④利用函数

是偶函数,又在区间

上递增,结合函数的周期性可以判断其正误.
解答:∵f(x+1)=-f(x),可得f(x+2)=f(x),∴函数f(x)是周期函数,①正确;
∵

是偶函数,∴f(-x+

)=

,令-x+

=t,有f(t)=f(1-t),∴有f(x)=f(1-x);(1)
又f(x+1)=-f(x),∴f(-x+1)=-f(-x),(2),由(1)(2)得-f(-x)=f(x),即f(-x)=-f(x),
∴函数f(x)是奇函数;②正确;
设P(x
0,y
0)为y=f(x)上任意一点,点P关于(1,0)的对称点为P′(2-x
0,-y
0),由①②正确可知,
f(2-x
0)=f(-x
0)=-f(x
0)=-y
0,即P′(2-x
0,-y
0)也在y=f(x)上,即函数f(x)图象关于点(1,0)对称,③正确;
∵函数

是偶函数,又在区间

上递增,∴f(x)在

上递减,又f(x+2)=f(x),∴函数f(x)在区间
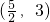
上递减,④正确;
故答案为:①②③④.
点评:本题考查函数奇偶性的性质,难点在于对抽象函数y=f(x)函数奇偶性的判断,考查学生的综合分析与转化能力,属于难题.

 是偶函数又在区间
是偶函数又在区间 上递增.给出四个命题:①函数f(x)是周期函数;②函数f(x)是奇函数;③函数f(x)图象关于点(1,0)对称;④函数f(x)在区间
上递增.给出四个命题:①函数f(x)是周期函数;②函数f(x)是奇函数;③函数f(x)图象关于点(1,0)对称;④函数f(x)在区间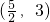 上递减.其中所有正确命题的序号是________.
上递减.其中所有正确命题的序号是________. 是偶函数,采用换元法,结合周期性可判断其奇偶性;
是偶函数,采用换元法,结合周期性可判断其奇偶性; 是偶函数,又在区间
是偶函数,又在区间 上递增,结合函数的周期性可以判断其正误.
上递增,结合函数的周期性可以判断其正误. 是偶函数,∴f(-x+
是偶函数,∴f(-x+ )=
)= ,令-x+
,令-x+ =t,有f(t)=f(1-t),∴有f(x)=f(1-x);(1)
=t,有f(t)=f(1-t),∴有f(x)=f(1-x);(1) 是偶函数,又在区间
是偶函数,又在区间 上递增,∴f(x)在
上递增,∴f(x)在 上递减,又f(x+2)=f(x),∴函数f(x)在区间
上递减,又f(x+2)=f(x),∴函数f(x)在区间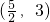 上递减,④正确;
上递减,④正确;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案