
【题目】如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径. 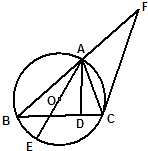
(1)求证:ACBC=ADAE;
(2)过点C作⊙O的切线交BA的延长线于点F,若AF=3,CF=9,求AC的长.
【答案】
(1)证明:如图所示,连接BE
∵AE是⊙O的直径,∴∠ABE=90°.
又∠E=∠ACB.
∵AD⊥BC,∠ADC=90°.
∴△ABE∽△ADC,∴ ![]() ,∴ABAC=ADAE.
,∴ABAC=ADAE.
又AB=BC,∴BCAC=ADAE.
(2)解:∵CF是⊙O的切线,∴CF2=AFBF,
∵AF=3,CF=9,∴92=3BF,解得BF=27.
∴AB=BF﹣AF=24.
∵∠ACF=∠FBC,∠CFB=∠AFC,∴△AFC∽△CFB,
∴ ![]() =
= ![]() ,∴AC=
,∴AC= ![]() =8.
=8.
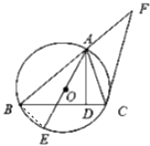
【解析】(1)如图所示,连接BE.由于AE是⊙O的直径,可得∠ABE=90°.利用∠E=∠ACB.进而得到△ABE∽△ADC,即可得到.(2)利用切割线定理可得CF2=AFBF,可得BF.再利用△AFC∽△CFB,可得 ![]() =
= ![]() ,即可得出.
,即可得出.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x)=  ,有下列5个结论: ①任取x1 , x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;
,有下列5个结论: ①任取x1 , x2∈[0,+∞),都有|f(x1)﹣f(x2)|≤2;
②函数y=f(x)在区间[4,5]上单调递增;
③f(x)=2kf(x+2k)(k∈N+),对一切x∈[0,+∞)恒成立;
④函数y=f(x)﹣ln(x﹣1)有3个零点;
⑤若关于x的方程f(x)=m(m<0)有且只有两个不同实根x1 , x2 , 则x1+x2=3.
则其中所有正确结论的序号是 . (请写出全部正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(πx+ ![]() )和函数g(x)=cos(πx+
)和函数g(x)=cos(πx+ ![]() )在区间[﹣
)在区间[﹣ ![]() ,
, ![]() ]上的图象交于A,B,C三点,则△ABC的面积是( )
]上的图象交于A,B,C三点,则△ABC的面积是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m>1,直线l:x﹣my﹣ ![]() =0,椭圆C:
=0,椭圆C: ![]() +y2=1,F1、F2分别为椭圆C的左、右焦点. (Ⅰ)当直线l过右焦点F2时,求直线l的方程;
+y2=1,F1、F2分别为椭圆C的左、右焦点. (Ⅰ)当直线l过右焦点F2时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,△AF1F2 , △BF1F2的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=f(x)的图象向右平移 ![]() 单位得到函数y=cos2x的图象,则f(x)=( )
单位得到函数y=cos2x的图象,则f(x)=( )
A.﹣sin2x
B.cos2x
C.sin2x
D.﹣cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2,点M在PD上.
,PA=2,点M在PD上. 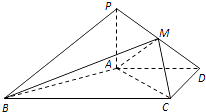
(1)求证:AB⊥PC
(2)若二面角M﹣AC﹣D的大小为45°,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在的安卓手机盛行一款“心有灵犀”的猜数字游戏,具体的规则如下:
玩家随机输入0~5中的三位数字(数字不重复),按“OK”键确定答案是否正确,手机会给出“xAyB”的提示,其中“xA”表示你输入的三位数字中,有“x”个数字和位置都与答案相同,其中“yB”表示你输入的三位数字中,有“y”个数字与答案相同,但是位置不同,例如:答案为“012”,当你输入“132”时会显示:“1A1B”.
(1)当你第一次输入时,手机显示“1A1B”的概率为多少?
(2)当你第一次输入时,且手机显示“xA2B”时,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com