
【题目】已知函数![]() (
(![]() 是自然对数的底数),
是自然对数的底数),![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,其中
,其中![]() 为
为![]() 的导函数,证明:对任意
的导函数,证明:对任意![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】2016年1月2日凌晨某公司公布的元旦全天交易数据显示,天猫元旦当天全天的成交金额为315.5亿元.为了了解网购者一次性购物情况,某统计部门随机抽查了1月1日100名网购者的网购情况,得到如下数据统计表,已知网购金额在2000元以上(不含2000元)的频率为0.4.
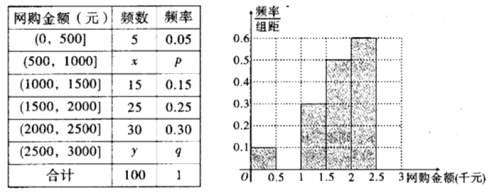
(I)先求出![]() 的值,再将如图4所示的频率分布直方图绘制完整;
的值,再将如图4所示的频率分布直方图绘制完整;
(II)对这100名网购者进一步调查显示:购物金额在2000元以上的购物者中网龄3年以上的有35人,
购物金额在2000元以下(含2000元)的购物者中网龄不足3年的有20人,请填写下面的列联表,并据
此判断能否在犯错误的概率不超过0.025的前提下认为网购金额超过2000元与网龄在3年以上有关?
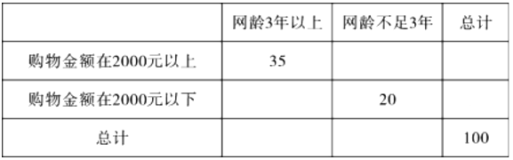
参考数据:

参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]()
![]() 为平面上的动点,且过点
为平面上的动点,且过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,满足:
,满足:![]()
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)在轨迹![]() 上求一点
上求一点![]() ,使得
,使得![]() 到直线
到直线![]() 的距离最短,并求出最短距离.
的距离最短,并求出最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的标准方程是![]()
(Ⅰ)求它的焦点坐标和准线方程;
(Ⅱ)直线![]() 过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高
吨,且每吨原材料创造的利润提高![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元
万元![]() .
.
(1)若设备升级后生产这批![]() 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批![]() 产品的利润,求
产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批![]() 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批![]() 产品的利润,求
产品的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,圆
,圆![]() .
.
(1)若过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)圆![]() 是以1为半径,圆心在圆
是以1为半径,圆心在圆![]() :
:![]() 上移动的动圆 ,若圆
上移动的动圆 ,若圆![]() 上任意一点
上任意一点![]() 分别作圆
分别作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若动圆![]() 同时平分圆
同时平分圆![]() 的周长、圆
的周长、圆![]() 的周长,则动圆
的周长,则动圆![]() 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q>1,且满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log![]() ,Sn=b1+b2+…+bn,求使
,Sn=b1+b2+…+bn,求使![]() 成立的正整数n的最大值.
成立的正整数n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的公比为q,其前n项的积为Tn,并且满足条件a1>1,a49a50-1>0,(a49-1)(a50-1)<0.给出下列结论:
①0<q<1;②a1a99-1<0;③T49的值是Tn中最大的;④使Tn>1成立的最大自然数n等于98.
其中所有正确结论的序号是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com