
【题目】已知函数f(x)=x3+x﹣16,
(1)求曲线y=f(x)在点(2,﹣6)处的切线的方程.
(2)如果曲线y=f(x)的某一切线与直线y=﹣ ![]() x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.
【答案】
(1)解:∵f(2)=23+2﹣16=﹣6,∴点(2,﹣6)在曲线上.
∵f′(x)=(x3+x﹣16)′=3x2+1,
∴在点(2,﹣6)处的切线的斜率为k=f′(2)=3×22+1=13.
∴切线的方程为y=13(x﹣2)+(﹣6),即y=13x﹣32
(2)解:∵切线与直线y=﹣ ![]() +3垂直,
+3垂直,
∴斜率k=4,∴设切点为(x0,y0),
则f′(x0)=3x ![]() +1=4,
+1=4,
∴x0=±1,
x0=1时,y0=﹣14;x0=﹣1,y0=﹣18,
即切点坐标为(1,﹣14)或(﹣1,﹣18).
切线方程为y=4(x﹣1)﹣14或y=4(x+1)﹣18.
即y=4x﹣18或y=4x﹣14
【解析】(1)确定点(2,﹣6)在曲线上,求导函数,可得切线斜率,从而可得切线方程;(2)利用曲线y=f(x)的某一切线与直线y=﹣ ![]() x+3垂直,可得斜率的积为﹣1,从而可求切点坐标与切线的方程.
x+3垂直,可得斜率的积为﹣1,从而可求切点坐标与切线的方程.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)的右焦点F(1,0),离心率为
(a>b>0)的右焦点F(1,0),离心率为 ![]() ,过F作两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N.
,过F作两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N. 
(1)求椭圆的方程;
(2)证明:直线MN必过定点,并求出此定点坐标;
(3)若弦AB,CD的斜率均存在,求△FMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为t1小时,其余工人加工完乙型装置所需时间为t2小时.
设f(x)=t1+t2.
(Ⅰ)求f(x)的解析式,并写出其定义域;
(Ⅱ)当x等于多少时,f(x)取得最小值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点. 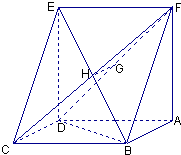
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ![]() ,求四棱锥F﹣ABCD的体积.
,求四棱锥F﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln x+![]() (a>0).
(a>0).
(1)求函数f(x)的极值;
(2)若对任意的x>0,恒有ax(2-ln x)≤1,求实数a的取值范围;
(3)是否存在实数a,使得函数f(x)在[1,e]上的最小值为0?若存在,试求出a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com