
����Ŀ������̨���żס�������������,ÿ�β���������ʱ,��Ҫ���Ź��.��֪ÿ�β��żס�������������ʱ,�����粥��ʱ������沥��ʱ���������˴����±���ʾ��
������ | �����粥��ʱ��/min | ��沥��ʱ��/min | �����˴�/���� |
�� | 70 | 5 | 60 |
�� | 60 | 5 | 25 |
����̨ÿ�ܰ��ŵļס�����������ܲ���ʱ��������![]() ,�����ܲ���ʱ��������
,�����ܲ���ʱ��������![]() ,�Ҽ������粥�ŵĴ����������������粥�Ŵ�����2��,�ֱ���
,�Ҽ������粥�ŵĴ����������������粥�Ŵ�����2��,�ֱ���![]() ,
,![]() ��ʾÿ�ܼƻ������ļס�������������Ĵ���,Ҫʹ�������˴����,�����̨ÿ�ܲ����ס�������������Ĵ����ֱ�Ϊ�� ��
��ʾÿ�ܼƻ������ļס�������������Ĵ���,Ҫʹ�������˴����,�����̨ÿ�ܲ����ס�������������Ĵ����ֱ�Ϊ�� ��
A.6,3B.5,2C.4,5D.2,7
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵx-O-y�У���֪����E��![]() (tΪ����)
(t����)
(1)�ڼ�����ϵO-x�У���A��B��CΪE�ϰ���ʱ�����е������㣬��ABCΪ�������Σ�����A��ļ��Ǧ�=![]() ����B��C����ļ����ꣻ
����B��C����ļ����ꣻ
(2)��ֱ������ϵx-O-y�У���֪����P��Q��������E�ϣ���Ӧ�����ֱ�Ϊt������t��2�� (0������2��)��MΪPQ���е㣬�� |MO| ��ȡֵ��Χ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ���㣺�����䶨����
���㣺�����䶨����![]() �ڵ��κ�һ���Ա���
�ڵ��κ�һ���Ա���![]() �����к���ֵ
�����к���ֵ![]() ����ƺ���
����ƺ���![]() ��
��![]() �Ϸ��.
�Ϸ��.
��1�����������![]() ��
��![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() �����ж�������Щ��
�����ж�������Щ��![]() �Ϸ�գ���˵������.
�Ϸ�գ���˵������.
��2��������![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ���Ƿ����ʵ��
���Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() ���䶨����
���䶨����![]() �Ϸ�գ������ڣ��������
�Ϸ�գ������ڣ��������![]() ��ֵ��������֤�����������ڣ���˵������.
��ֵ��������֤�����������ڣ���˵������.
��3����֪����![]() ���䶨����
���䶨����![]() �Ϸ�գ��ҵ�����������
�Ϸ�գ��ҵ�����������![]() ��
��![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
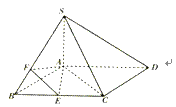
����Ŀ����ͼ��ʾ������S��ABCD�У��ı���ABCDΪƽ���ı��Σ�BA��AC��SA��AD��SC��CD��
������֤��AC��SB��
������AB��AC��SA��3��EΪ�߶�BC���е㣬FΪ�߶�SB�Ͽ���B�����ȷֵ㣬��ֱ��SC��ƽ��AEF���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������ÿ�ˮ���ݣ�����������������£����Ƚ�ˮ���ȵ�100![]() ��ˮ��
��ˮ��![]() ��ʱ��
��ʱ��![]() ��������һ�κ�����ϵ�����ÿ�ˮ���������ݺ��������·��ã��¶�
��������һ�κ�����ϵ�����ÿ�ˮ���������ݺ��������·��ã��¶�![]() ��ʱ��
��ʱ��![]() �������㺯���Ĺ�ϵʽΪ
�������㺯���Ĺ�ϵʽΪ ![]() ��
��![]() Ϊ������, ͨ������������40
Ϊ������, ͨ������������40![]() ʱ���ڸ���ѣ�ij������Ϊ
ʱ���ڸ���ѣ�ij������Ϊ![]() ʱ�����������IJ���������ͼ��ʾ����ô���������̳���һ�����������ڿڸ����ʱ���ã�������Ҫ��ʱ��Ϊ
ʱ�����������IJ���������ͼ��ʾ����ô���������̳���һ�����������ڿڸ����ʱ���ã�������Ҫ��ʱ��Ϊ

A. 35![]() B. 30
B. 30![]()
C. 25![]() D. 20
D. 20![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy��ֱ��![]() ��������C��
��������C��![]() ����A��B���㣬��
����A��B���㣬��![]() ��
��
![]() ��C�ķ��̣�
��C�ķ��̣�
![]() ��DΪֱ��
��DΪֱ��![]() ��һ�㣬��
��һ�㣬��![]() ������M��C�ϣ���M�����꣮
������M��C�ϣ���M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������
������![]() ��
��
��������![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��������![]() ������
������![]() �ϵ���Сֵ��
�ϵ���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԲC��![]() ��
��![]() ��1(a>b>0)��������Ϊ
��1(a>b>0)��������Ϊ![]() ����Բ�϶���P��һ������ľ������СֵΪ3(
����Բ�϶���P��һ������ľ������СֵΪ3(![]() ��1)��
��1)��
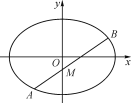
(1) ����ԲC�ı����̣�
(2) ��֪����M(0����1)�Ķ�ֱ��l����ԲC����A��B���㣬���ж����߶�ABΪֱ����Բ�Ƿ������㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������㣬Ϊ�˱�֤��õ������ʣ��㱻���ϰ���Ҫ����̵�ʱ���ڽ���ּ���أ�������ʱ����������������ܿ��ʧȥ���ʶȣ��������ڵ����װ����Ķ�����ȷ��������ʶ�.���װ���һ�ֻӷ��Լ������ǰ��������������ϸ���ֽ������.���װ������۾ͱ���������ʶ��½������忪ʼ���ʽ������ܣ�.��֪ij����ʧȥ�����ʶ�![]() ���������ʱ��
���������ʱ��![]() ���֣�����ĺ�����ϵʽΪ
���֣�����ĺ�����ϵʽΪ![]() .��������10���ӣ�������ʧȥ�����ʶ�Ϊ10%��������20���ӣ�������ʧȥ�����ʶ�Ϊ20%����ô������ʱ���������������������ڶʱ���ʼʧȥȫ�����ʶȣ���֪
.��������10���ӣ�������ʧȥ�����ʶ�Ϊ10%��������20���ӣ�������ʧȥ�����ʶ�Ϊ20%����ô������ʱ���������������������ڶʱ���ʼʧȥȫ�����ʶȣ���֪![]() �����ȡ�������� ��
�����ȡ�������� ��
A.33����B.40����C.43����D.50����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com