
 =λ,求λ的取值范围.
=λ,求λ的取值范围.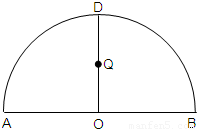
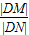 =λ可得λ与k的关系式,借助k的范围即可求得λ范围,注意M点位于中间;当直线不存在斜率k时,易求λ值,综上即可求得范围.
=λ可得λ与k的关系式,借助k的范围即可求得λ范围,注意M点位于中间;当直线不存在斜率k时,易求λ值,综上即可求得范围. 解 (1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,?
解 (1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,? >|AB|=4,
>|AB|=4, ,
, ,c=2,b=1,∴曲线C的方程为
,c=2,b=1,∴曲线C的方程为 +y2=1;
+y2=1;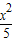 +y2=1,
+y2=1, ,
, =λ,由韦达定理得
=λ,由韦达定理得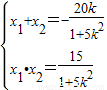 ,
, ,
,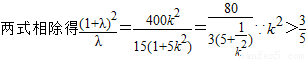 ,
, ,∴5<
,∴5< +5<
+5< ,∴4<
,∴4<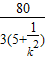 <
< ,即4<
,即4<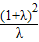 <
< ,
, <λ<3,∵λ=
<λ<3,∵λ=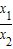 =
= ,M在D、N之间,∴λ<1,
,M在D、N之间,∴λ<1, =
= (此时直线与y轴重合),
(此时直线与y轴重合), <1..
<1..

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
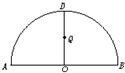 如图,
如图, |
| ADB |
| DM |
| DN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ADB为半圆,AB为直径,O为圆心,
如图,ADB为半圆,AB为直径,O为圆心,| AB |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
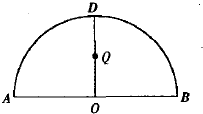 如图,
如图, |
| ADB |
| EM |
| MB |
| EN |
| NB |
查看答案和解析>>
科目:高中数学 来源: 题型:
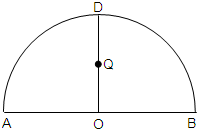 如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变
如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变| |DM| | |DN| |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
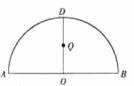
如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变。
(I)建立适当的平面直角坐标系,求曲线C的方程;
(II)过点B的直线l与曲线C交于M、N两点,与OD所在直线交于E点,
![]() 为定值。
为定值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com