
【题目】设V是空间中2019个点构成的集合,其中任意四点不共面某些点之间连有线段,记E为这些线段构成的集合.试求最小的正整数n,满足条件:若E至少有n个元素,则E一定含有908个二元子集,其中每个二元子集中的两条线段有公共端点,且任意两个二元子集的交为空集.
【答案】最小的n是2795
【解析】
先证明一个引理:设G=(V,E)是一个简单图,且G是连通的,则G含有![]() 个两两无公共边的角.再利用引理和反证法,结合组合数的凸性即可求得结果.
个两两无公共边的角.再利用引理和反证法,结合组合数的凸性即可求得结果.
为了叙述方便,称一个图中的两条相邻的边构成一个“角”,先证明一个引理:
设G=(V,E)是一个简单图,且G是连通的,
则G含有![]() 个两两无公共边的角(这里[a]表示实数a的整数部分).
个两两无公共边的角(这里[a]表示实数a的整数部分).
引理的证明:对E的元素个数|E|归纳证明.
当|E|=0,1,2,3时,结论显然成立.
下面假设|E|≥4,并且结论在|E|较小时均成立.
只需证明,在G中可以选取两条边a、b构成一个角,在G中删去a、b这两条边后,剩下的图含有一个连通分支包含|E|-2条边.
对这个连通分支应用归纳假设即得结论成立.
考虑G中的最长路![]() ,其中
,其中![]() 是互不相同的顶点.
是互不相同的顶点.
因为G连通,故k≥3.
情形1:![]() .
.
由于P是最长路,v1的邻点均在![]() 中,设
中,设![]() ,其中3≤i≤k.
,其中3≤i≤k.
则![]() 是一个角,在E中删去这两条边.
是一个角,在E中删去这两条边.
若v1处还有第三条边,则剩下的图是连通的;
若v1处仅有被删去的两条边,则v1成为孤立点,其余顶点仍互相连通.总之在剩下的图中有一个连通分支含有|E|-2条边.
情形2:![]() ,
,![]() .
.
则![]() 是一个角,在G中删去这两条边后,
是一个角,在G中删去这两条边后,![]() 都成为孤立点,其余的点互相连通,
都成为孤立点,其余的点互相连通,
因此有一个连通分支含有![]() 条边.
条边.
情形3:![]() ,且v2与
,且v2与![]() 中某个点相邻.
中某个点相邻.
则![]() 是一个角,在G中删去这两条边后,v1成为孤立点,其余点互相连通,
是一个角,在G中删去这两条边后,v1成为孤立点,其余点互相连通,
因此有一个连通分支含有![]() 条边.
条边.
情形4:![]() ,且v2与某个
,且v2与某个![]() 相邻.
相邻.
由于P是最长路,故u的邻点均在![]() 之中.
之中.
因![]() 是一个角,在G中删去这两条边,则v1是孤立点.
是一个角,在G中删去这两条边,则v1是孤立点.
若处仅有边uv2,则删去所述边后u也是孤立点,而其余点互相连通.
若u处还有其他边uvi,3≤i≤k,则删去所述边后,除v1外其余点互相连通.
总之,剩下的图中有一个连通分支含有![]() 条边.
条边.
引理获证.
回到原题,题中的V和E可看作一个图G=(V,E)
首先证明n≥2795.
设![]() .
.
在![]() 中,首先两两连边,再删去其中15条边(例如
中,首先两两连边,再删去其中15条边(例如![]() ),共连了
),共连了![]() 条边,则这61个点构成的图是连通图.再将剩余的201-61=1958个点配成979对,每对两点之间连一条边,则图G中一共连了1815+979=2794条线段.
条边,则这61个点构成的图是连通图.再将剩余的201-61=1958个点配成979对,每对两点之间连一条边,则图G中一共连了1815+979=2794条线段.
由上述构造可见,G中的任何一个角必须使用![]() 相连的边,
相连的边,
因此至多有![]() 个两两无公共边的角.
个两两无公共边的角.
故满足要求的n不小于2795.
另一方面,若|E|≥2795,可任意删去若干条边,只考虑![]() 的情形.
的情形.
设G有k个连通分支,分别有![]() 个点,及
个点,及![]() 条边.
条边.
下面证明![]() 中至多有979个奇数.
中至多有979个奇数.
反证法,假设![]() 中有至少980个奇数由于
中有至少980个奇数由于![]() 是奇数,
是奇数,
故![]() 中至少有981个奇数,k≥981.
中至少有981个奇数,k≥981.
不妨设![]() 都是奇数,显然
都是奇数,显然![]() .
.
令![]() ,则有
,则有![]() ,
,
故![]() ①
①
利用组合数的凸性,即对x≥y≥3,有![]() ,
,
可知当m1,…,m980,m由980个2以及一个59构成时,![]() 取得最大值.
取得最大值.
于是![]() ,
,
这与①矛盾.从而![]() 中至多有979个奇数.
中至多有979个奇数.
对每个连通分支应用引理,可知G中含有N个两两无公共边的角,
其中![]() .
.
综上,所求最小的n是2795.


科目:高中数学 来源: 题型:
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.28 | 4.72 | 3.58 | 2.70 | 2.15 |
倒闭企业所占比例 | 21.4% | 19.1% | 14.5% | 10.9% | 8.7% |
(1)由所给数据可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测
的回归方程,预测![]() 年成立的企业中倒闭企业所占比例.
年成立的企业中倒闭企业所占比例.
参考数据:![]() ,
,![]() ,
,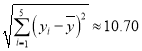 ,
,![]() ,
,
相关系数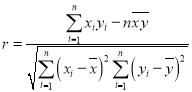 ,样本
,样本![]() 的最小二乘估计公式为
的最小二乘估计公式为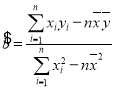 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是一个首项为2,公比为q(q![]() 1)的等比数列,且3a1,2a2,a3成等差数列.
1)的等比数列,且3a1,2a2,a3成等差数列.
(1)求{an}的通项公式;
(2)已知数列{bn}的前n项和为Sn,b1=1,且![]() 1(n≥2),求数列{an
1(n≥2),求数列{an![]() bn}的前n项和Tn.
bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是椭圆![]() 的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
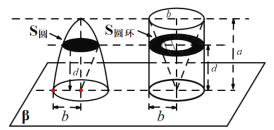
【题目】我国南北朝时期的数学家祖暅提出了一条原理:“幂势既同,则积不容异”即夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.椭球是椭圆绕其长轴旋转所成的旋转体,如图,将底面半径都为![]() .高都为
.高都为![]() 的半椭球和已被挖去了圆锥的圆柱(被挖去的圆锥以圆柱的上底面为底面,下底面的圆心为顶点)放置于同一平面
的半椭球和已被挖去了圆锥的圆柱(被挖去的圆锥以圆柱的上底面为底面,下底面的圆心为顶点)放置于同一平面![]() 上,用平行于平面
上,用平行于平面![]() 且与平面
且与平面![]() 任意距离
任意距离![]() 处的平面截这两个几何体,截面分别为圆面和圆环,可以证明
处的平面截这两个几何体,截面分别为圆面和圆环,可以证明![]() 圆=
圆=![]() 圆环总成立.据此,椭圆的短半轴长为2,长半轴长为4的椭球的体积是( )
圆环总成立.据此,椭圆的短半轴长为2,长半轴长为4的椭球的体积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于函数
,对于函数![]() 有下述四个结论:①函数
有下述四个结论:①函数![]() 在其定义域上为增函数;②对于任意的
在其定义域上为增函数;②对于任意的![]() ,
,![]() ,都有
,都有![]() 成立;③
成立;③![]() 有且仅有两个零点;④若
有且仅有两个零点;④若![]() ,则
,则![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线为同一直线.其中所有正确的结论有( )
处的切线为同一直线.其中所有正确的结论有( )
A.①②③B.①③C.②③④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷![]() 广元某景点设有共享电动车租车点,共享电动车的收费标准是每小时2元
广元某景点设有共享电动车租车点,共享电动车的收费标准是每小时2元![]() 不足1小时的部分按1小时计算
不足1小时的部分按1小时计算![]() 甲、乙两人各租一辆电动车,若甲、乙不超过一小时还车的概率分别为
甲、乙两人各租一辆电动车,若甲、乙不超过一小时还车的概率分别为![]() ;一小时以上且不超过两小时还车的概率分别为
;一小时以上且不超过两小时还车的概率分别为![]() ;两人租车时间都不会超过三小时.
;两人租车时间都不会超过三小时.
![]() Ⅰ
Ⅰ![]() 求甲、乙两人所付租车费用相同的概率;
求甲、乙两人所付租车费用相同的概率;
![]() Ⅱ
Ⅱ![]() 设甲、乙两人所付的租车费用之和为随机变量
设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com