
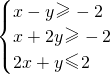 ,若O为坐标原点,M(x,y),N(1,-2),则
,若O为坐标原点,M(x,y),N(1,-2),则 •
• 的最小值是________.
的最小值是________. •
• 的表达式,利用线性规划知识求线性目标函数的最小值.
的表达式,利用线性规划知识求线性目标函数的最小值.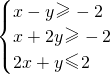 得可行域为△ABC的边界及其内部,如图,
得可行域为△ABC的边界及其内部,如图,
 =(x,y),
=(x,y), =(1,-2).
=(1,-2). •
• =x-2y.
=x-2y. •
• =x-2y,则
=x-2y,则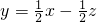 ,
,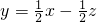 在y轴上的截距最大.
在y轴上的截距最大.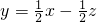 过点A(0,2)时截距最大,
过点A(0,2)时截距最大, •
• 的最小值是-4.
的最小值是-4.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com