Question

已知函数f（x）=ax³+bx²+cx在x=±1处取得极值，且在x=0处的切线的斜率为-3．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若过点A（2，m）可作曲线y=f（x）的三条切线，求实数m的取值范围．

Answer 1

分析：（Ⅰ）由函数f（x）=ax³+bx²+cx在x=±1处取得极值，且在x=0处的切线的斜率为-3，求导，可得±1是f′（x）=0的两根，且f′（0）=-3，解方程组即可求得，a，b，c的值，从而求得f（x）的解析式；（Ⅱ）设切点，求切线方程，得到m=-2x₀³+6x₀²-6，要求过点A（2，m）可作曲线y=f（x）的三条切线，即求m=-2x₀³+6x₀²-6有三个零点，画出函数的草图，即可求得
实数m的取值范围．

解答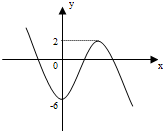：解：（Ⅰ）f'（x）=3ax²+2bx+c
依题意

f′(1)=3a+2b+c=0 f′(-1)=3a-2b+c=0

?

b=0 3a+c=0

又f'（0）=-3∴c=-3∴a=1∴f（x）=x³-3x
（Ⅱ）设切点为（x₀，x₀³-3x₀），
∵f'（x）=3x²-3∴f'（x₀）=3x₀²-3
∴切线方程为y-（x₀³-3x₀）=（3x₀²-3）（x-x₀）
又切线过点A（2，m）
∴m-（x₀³-3x₀）=（3x₀²-3）（2-x₀）
∴m=-2x₀³+6x₀²-6
令g（x）=-2x³+6x²-6
则g'（x）=-6x²+12x=-6x（x-2）
由g'（x）=0得x=0或x=2g（x）_极小值=g（0）=-6，g（x）_极大值=g（2）=2
画出草图知，当-6＜m＜2时，m=-2x³+6x²-6有三解，
所以m的取值范围是（-6，2）．

点评：此题是中档题．考查利用导数研究函数的单调性和极值问题，和利用导数研究曲线上某点的切线问题，体现了数形结合和转化的思想，考查了学生灵活应用知识分析解决问题的能力．