
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点![]() 的极坐标为
的极坐标为![]() ,圆
,圆![]() 以
以![]() 为圆心,4为半径;又直线
为圆心,4为半径;又直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(Ⅰ)求直线![]() 和圆
和圆![]() 的普通方程;
的普通方程;
(Ⅱ)试判定直线![]() 和圆
和圆![]() 的位置关系.若相交,则求直线
的位置关系.若相交,则求直线![]() 被圆
被圆![]() 截得的弦长.
截得的弦长.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
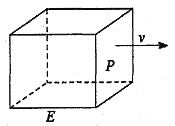
【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为![]() ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为![]() 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与![]() ×S成正比,比例系数为
×S成正比,比例系数为![]() ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为![]() ,记
,记![]() 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=![]() 时。
时。
(1)写出![]() 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度![]() ,使总淋雨量
,使总淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列![]() 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1-![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.

(1)写出服药后y与t之间的函数关系式;
(2)据测定,每毫升血液中含药量不少于4 μg时治疗疾病有效,假若某病人一天中第一次服药为上午7:00,问:一天中怎样安排服药时间(共4次)效果最佳?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]()
![]() 的公共点的轨迹为曲线
的公共点的轨迹为曲线![]() ,且曲线
,且曲线![]() 与
与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() .若曲线
.若曲线![]() 上相异两点
上相异两点![]() 满足直线
满足直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)证明直线![]() 恒过定点,并求定点的坐标.
恒过定点,并求定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司从1999年的年产值100万元,增加到10年后2009年的500万元,如果每年产值增长率相同,则每年的平均增长率是多少?(ln(1+x)≈x,lg2=0.3,ln10=2.30)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图,当输入的x的值为0和4时,输出的值相等,根据该图和下列各小题的条件解答下面的几个问题.

(1)该程序框图解决的是一个什么问题?
(2)当输入的x的值为3时,求输出的f(x)的值;
(3)要想使输出的值最大,求输入的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com