
【题目】如图,在正方体![]() 中,平面
中,平面![]() 与正方体的各个面所在的平面所成的二面角的大小分别是多少?
与正方体的各个面所在的平面所成的二面角的大小分别是多少?

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知不等式ax2-5x+b>0的解是-3<x<2,设A={x|bx2-5x+a>0},B={x|![]() }.
}.
(1)求a,b的值;
(2)求A∩B和A∪(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知l,m是平面![]() 外的两条不同直线.给出下列三个论断:
外的两条不同直线.给出下列三个论断:
①l⊥m;②m∥![]() ;③l⊥
;③l⊥![]() .
.
以其中的两个论断作为条件,余下的一个论断作为结论,则三个命题中正确命题的个数为( )个.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,加快水污染防治,建设美丽中国![]() 根据环保部门对某河流的每年污水排放量
根据环保部门对某河流的每年污水排放量![]() 单位:吨
单位:吨![]() 的历史统计数据,得到如下频率分布表:
的历史统计数据,得到如下频率分布表:
污水量 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
(Ⅰ)求在未来3年里,至1年污水排放量![]() 的概率;
的概率;
(Ⅱ)该河流的污水排放对沿河的经济影响如下:当![]() 时,没有影响;当
时,没有影响;当![]() 时,经济损失为10万元;当
时,经济损失为10万元;当![]() 时,经济损失为60万元
时,经济损失为60万元![]() 为减少损失,现有三种应对方案:
为减少损失,现有三种应对方案:
方案一:防治350吨的污水排放,每年需要防治费![]() 万元;
万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种方案,哪种方案好,并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
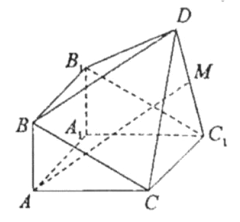
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年吴京执导的动作、军事电影《战狼2》上映三个月,以![]() 亿震撼世界的票房成绩圆满收官,该片也是首部跻身全球票房TOP100的中国电影.小明想约甲、乙、丙、丁四位好朋友一同去看《战狼2》,并把标识分别为A、B、C、D的四张电影票放在编号分别为
亿震撼世界的票房成绩圆满收官,该片也是首部跻身全球票房TOP100的中国电影.小明想约甲、乙、丙、丁四位好朋友一同去看《战狼2》,并把标识分别为A、B、C、D的四张电影票放在编号分别为![]() ,
,![]() ,
,![]() ,
,![]() 的四个不同盒子里,让四位好朋友进行猜测:
的四个不同盒子里,让四位好朋友进行猜测:
甲说:第![]() 个盒子里面放的是B,第
个盒子里面放的是B,第![]() 个盒子里面放的是C;
个盒子里面放的是C;
乙说:第![]() 个盒子里面放的是B,第
个盒子里面放的是B,第![]() 个盒子里面放的是D;
个盒子里面放的是D;
丙说:第![]() 个盒子里面放的是D,第
个盒子里面放的是D,第![]() 个盒子里面放的是C;
个盒子里面放的是C;
丁说:第![]() 个盒子里面放的是A,第
个盒子里面放的是A,第![]() 个盒子里面放的是C.
个盒子里面放的是C.
小明说:“四位朋友,你们都只说对了一半.”
可以推测,第![]() 个盒子里面放的电影票为__________.
个盒子里面放的电影票为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),

(1)由图中数据求a的值;
(2)若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为多少?
(3)估计这所小学的小学生身高的众数,中位数(保留两位小数)及平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 均为真命题,则命题
均为真命题,则命题![]() 为真命题
为真命题
B. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ”
”
C. 在![]() ,“
,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D. 命题![]() “
“![]() ”的否定为
”的否定为![]() “
“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“珠算之父”程大为是我国明代伟大数学家,他的应用数学巨著《算法统综》的问世,标志着我国的算法由筹算到珠算转变的完成,程大位在《算法统综》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上稍四节储三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”((注)三升九:![]() 升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
A.![]() 升B.
升B.![]() 升C.
升C.![]() 升D.
升D.![]() 升
升
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com