
分析 令g(x)=$\frac{xcosx+sinx}{cosx+2}$,则f(x)=g(x)+1,g(x)是奇函数,它的最大值为M-1,它的最小值为m-1,再根据奇函数的性质可得M-1+m-1=0,由此求得M+m的值.
解答 解:∵函数f(x)=$\frac{xcosx+cosx+sinx+2}{cosx+2}$=$\frac{xcosx+sinx}{cosx+2}$+1,令g(x)=$\frac{xcosx+sinx}{cosx+2}$,则f(x)=g(x)+1,
显然,g(x)是奇函数,它的最大值为M-1,它的最小值为m-1,再根据奇函数的性质可得M-1+m-1=0,
故有M+m=2,
故答案为:2.
点评 本题主要考查函数的奇偶性的应用,根据奇函数的最大值与最小值的和等于零,求得M+m的值,属于基础题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
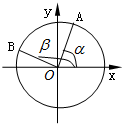 如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.
如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{6}π$ | B. | $\frac{5}{4}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{5}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,相距14km的两个居民小区M和N位于河岸l(直线)的同侧,M和N距离河岸分别为10km和8km.现要在河的小区一侧选一地点P,在P处建一个生活污水处理站,从P排直线水管PM,PN分别到两个小区和垂直于河岸的水管PQ,使小区污水经处理后排入河道.设PQ段长为t km(0<t<8).
如图,相距14km的两个居民小区M和N位于河岸l(直线)的同侧,M和N距离河岸分别为10km和8km.现要在河的小区一侧选一地点P,在P处建一个生活污水处理站,从P排直线水管PM,PN分别到两个小区和垂直于河岸的水管PQ,使小区污水经处理后排入河道.设PQ段长为t km(0<t<8).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com