
【题目】已知数列{an}的前n项和为Sn,且Sn=n(n+2)(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】(1)an=2n+1;(2)Tn![]() .
.
【解析】
(1)由n=1时求得a1,当n≥2时,由Sn=n(n+2)(n∈N*)① ,
可得Sn﹣1=(n﹣1)(n+1)② ,由①﹣②得an=2n+1,再检验当n=1时是否适合,求得an;
(2)由(1)求得bn![]() ,再利用错位相减法求其前n项和Tn即可.
,再利用错位相减法求其前n项和Tn即可.
解:(1)由题知:当n=1时,有S1=1×3=3=a1;
当n≥2时,由Sn=n(n+2)(n∈N*)① ,
可得Sn﹣1=![]() ② ,由①﹣② 得an=2n+1,
② ,由①﹣② 得an=2n+1,
又n=1时也适合,故an=2n+1;
(2)由(1)知bn![]() ,
,
∵Tn=3![]() 5
5![]() 7×(
7×(![]() )3+…+(2n+1)(
)3+…+(2n+1)(![]() )n③,
)n③,
∴![]() 3
3![]() 5×(
5×(![]() )3+…+(2n+1)
)3+…+(2n+1)![]() ④,
④,
由③﹣④可得:![]()

![]() ,
,
所以Tn![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:
【题目】年前某市质监部门根据质量管理考核指标对本地的500家食品生产企业进行考核,然后通过随机抽样抽取其中的50家,统计其考核成绩(单位:分),并制成如下频率分布直方图.
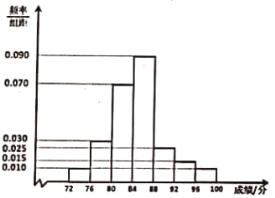
(1)求这50家食品生产企业考核成绩的平均数![]() (同一组中的数据用该组区间的中点值为代表)及中位数a(精确到0.01)
(同一组中的数据用该组区间的中点值为代表)及中位数a(精确到0.01)
(2)该市质监部门打算举办食品生产企业质量交流会,并从这50家食品生产企业中随机抽取4家考核成绩不低于88分的企业发言,记抽到的企业中考核成绩在![]() 的企业数为X,求X的分布列与数学期望
的企业数为X,求X的分布列与数学期望
(3)若该市食品生产企业的考核成绩X服从正态分布![]() 其中
其中![]() 近似为50家食品生产企业考核成绩的平均数
近似为50家食品生产企业考核成绩的平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() ,利用该正态分布,估计该市500家食品生产企业质量管理考核成绩高于90.06分的有多少家?(结果保留整数).
,利用该正态分布,估计该市500家食品生产企业质量管理考核成绩高于90.06分的有多少家?(结果保留整数).
附参考数据与公式:
![]()
![]()
则![]() ,
,![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆上的一个动点(不与左、右顶点重合),且
是椭圆上的一个动点(不与左、右顶点重合),且![]() 的周长为6,点
的周长为6,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,直线
,直线![]() 交于点
交于点![]() .
.
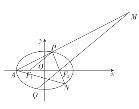
(1)求椭圆方程;
(2)若直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的侧棱和底面边长相等,在这个正四棱锥的
的侧棱和底面边长相等,在这个正四棱锥的![]() 条棱中任取两条,按下列方式定义随机变量
条棱中任取两条,按下列方式定义随机变量![]() 的值:
的值:
若这两条棱所在的直线相交,则![]() 的值是这两条棱所在直线的夹角大小(弧度制);
的值是这两条棱所在直线的夹角大小(弧度制);
若这两条棱所在的直线平行,则![]() ;
;
若这两条棱所在的直线异面,则![]() 的值是这两条棱所在直线所成角的大小(弧度制).
的值是这两条棱所在直线所成角的大小(弧度制).
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 中,
中,![]() 与
与![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() 平面
平面![]() .
.
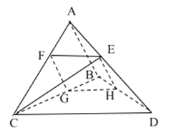
(1)求证:![]() ;
;
(2)过![]() 作一平面分别交
作一平面分别交![]() ,
, ![]() ,
, ![]() 于
于![]() ,
,![]() ,
,![]() ,若四边形
,若四边形![]() 为平行四边形,求多面体
为平行四边形,求多面体![]() 的表面积.
的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中某班共有40个学生,将学生的身高分成4组:平频率/组距![]() ,
,![]() ,
,![]() ,
,![]() 进行统计,作成如图所示的频率分布直方图.
进行统计,作成如图所示的频率分布直方图.
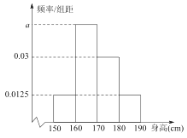
(1)求频率分布直方图中![]() 的值和身高在
的值和身高在![]() 内的人数;
内的人数;
(2)求这40个学生平均身高的估计值(同一组中的数据用该组区间的中点值为代表)(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及曲线C的参数方程;
的普通方程以及曲线C的参数方程;
(2)过曲线C上任意一点M作与直线![]() 的夹角为
的夹角为![]() 的直线,交
的直线,交![]() 于点N,求
于点N,求![]() 的最小值
的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com