
分析 由数量积的坐标运算结合两角和的余弦得答案.
解答 解:∵$\overrightarrow a=(cos{23°},cos{67°}),\overrightarrow b=(cos{53°},cos{37°})$,
∴$\overrightarrow a•\overrightarrow b$=cos23°cos53°+cos67°cos37°
=cos23°cos53°+sin23°sin53°=cos(23°-53°)
=cos(-30°)=cos30°=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{{\sqrt{3}}}{2}$.
点评 本题考查平面向量的数量积运算,考查两角和的余弦,是基础的计算题.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
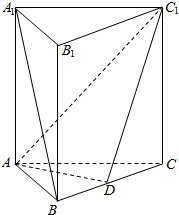 如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
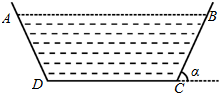 2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?
2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费指数(百元) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
| 人数 | 3 | 4 | 6 | 5 | 2 |
| 消费指数(百元) | [3,4) | [4,5) | [5,6) | [6,7) | [7,8] |
| 人数 | 9 | 36 | a | 54 | 9 |
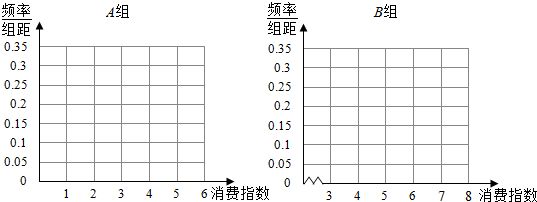
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com