
【题目】攀枝花是一座资源富集的城市,矿产资源储量巨大,已发现矿种76种,探明储量39种,其中钒、钛资源储量分别占全国的63%和93%,占全球的11%和35%,因此其素有“钒钛之都”的美称.攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值y(y值越大产品的性能越好)与这种新合金材料的含量x(单位:克)的关系为:当0≤x<7时,y是x的二次函数;当x≥7时,![]() .测得部分数据如表:
.测得部分数据如表:

(1)求y关于x的函数关系式y=f(x);
(2)求该新合金材料的含量x为何值时产品的性能达到最佳.
【答案】(1)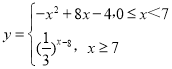 ;(2)当
;(2)当![]() 时产品的性能达到最佳
时产品的性能达到最佳
【解析】
(1)二次函数可设解析式为![]() ,代入已知数据可求得函数解析式;
,代入已知数据可求得函数解析式;
(2)分段函数分段求出最大值后比较可得.
(1)当0≤x<7时,y是x的二次函数,可设y=ax2+bx+c(a≠0),
由x=0,y=﹣4可得c=﹣4,由x=2,y=8,得4a+2b=12①,
由x=6,y=8,可得36a+6b=12②,联立①②解得a=﹣1,b=8,
即有y=﹣x2+8x﹣4;
当x≥7时,![]() ,由x=10,
,由x=10,![]() ,可得m=8,即有
,可得m=8,即有![]() ;
;
综上可得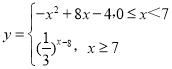 .
.
(2)当0≤x<7时,y=﹣x2+8x﹣4=﹣(x﹣4)2+12,
即有x=4时,取得最大值12;
当x≥7时,![]() 递减,可得y≤3,当x=7时,取得最大值3.
递减,可得y≤3,当x=7时,取得最大值3.
综上可得当x=4时产品的性能达到最佳.


科目:高中数学 来源: 题型:
【题目】已知A,B两地相距24km.甲车、乙车先后从A地出发匀速驶向B地.甲车从A地到B地需行驶25min;乙车从A地到B地需行驶20min.乙车比甲车晚出发2min.
(1)分别写出甲、乙两车所行路程关于甲车行驶时间的函数关系式;
(2)甲、乙两车何时在途中相遇?相遇时距A地多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=8x,圆M:(x-2)2+y2=4,点N为抛物线E上的动点,O为坐标原点,线段ON的中点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)点Q(x0,y0)(x0≥5)是曲线C上的点,过点Q作圆M的两条切线,分别与x轴交于A,B两点,求△QAB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个关于圆锥曲线的命题中:
①设![]() 为两个定点,
为两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
②方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
④已知抛物线![]() ,以过焦点的一条弦
,以过焦点的一条弦![]() 为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
为直径作圆,则此圆与准线相切,其中真命题为__________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α,β为两个不同平面,a,b为两条不同直线,下列选项正确的是( )
①若a∥α,b∥α,则a∥b
②若aα,α∥β,则a∥β
③若α∥β,a∥β,则![]()
④若a∥α,则a与平面α内的无数条直线平行
⑤若a∥b,则a平行于经过b的所有平面
A.①②B.③④C.②④D.②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在![]() 年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知
年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知![]() 的顶点
的顶点![]() 、
、![]() ,若其欧拉线方程为
,若其欧拉线方程为![]() ,则顶点
,则顶点![]() 的坐标是( )
的坐标是( )
参考公式:若![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 、
、![]() 、
、![]() ,则该
,则该![]() 的重心的坐标为
的重心的坐标为![]() .
.
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com