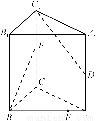
已知如图①所示，矩形纸片AA′A1′A1，点B、C、B1、C1分别为AA′、A1A1′的三等分点，将矩形纸片沿BB1、CC1折成如图②形状(正三棱柱)，若面对角线AB1⊥BC1，求证：A1C⊥AB1.
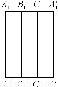
(图①)
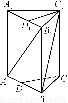
(图②)
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷（解析版） 题型：解答题
在直四棱柱ABCD-A1B1C1D1中，AA1＝2，底面是边长为1的正方形，E、F分别是棱B1B、DA的中点．
(1)求二面角D1-AE-C的大小；
(2)求证：直线BF∥平面AD1E.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷（解析版） 题型：解答题
在如图所示的多面体中，已知正三棱柱ABCA1B1C1的所有棱长均为2，四边形ABDC是菱形．
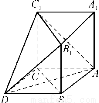
(1)求证：平面ADC1⊥平面BCC1B1；
(2)求该多面体的体积．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷（解析版） 题型：解答题
在空间四边形ABCD中，已知AC⊥BD,AD⊥BC,求证：AB⊥CD.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷（解析版） 题型：填空题
已知l，m是两条不同的直线，α、β是两个不同的平面，有下列四个命题：
①若l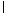
β，且α⊥β，则l⊥α；
②若l⊥β，且α∥β，则l⊥α；
③若l⊥β，且α⊥β，则l∥α；
④若α∩β＝m，且l∥m，则l∥α.
则所有正确的命题是________．(填序号)
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷（解析版） 题型：填空题
下列命题：①一条直线在平面内的射影是一条直线；②在平面内射影是直线的图形一定是直线；③在同一平面内的射影长相等，则斜线长相等；④两斜线与平面所成的角相等，则这两斜线互相平行．其中真命题的个数是________．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷（解析版） 题型：解答题
如图所示，在直三棱柱ABCA1B1C1中，D、E分别为AA1、CC1的中点，AC⊥BE，点F在线段AB上，且AB＝4AF.若M为线段BE上一点，试确定M在线段BE上的位置，使得C1D∥平面B1FM.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷（解析版） 题型：填空题
从正方体ABCD－A1B1C1D1的8个顶点中任意取4个不同的顶点，这4个顶点可能是：
(1)矩形的4个顶点；
(2)每个面都是等边三角形的四面体的4个顶点；
(3)每个面都是直角三角形的四面体的4个顶点；
(4)有三个面是等腰直角三角形，有一个面是等边三角形的四面体的4个顶点．
其中正确的结论有________个．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷（解析版） 题型：解答题
已知各项均为正数的等比数列{an}的公比为q，且0＜q＜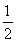
.
(1)在数列{an}中是否存在三项，使其成等差数列？说明理由；
(2)若a1＝1，且对任意正整数k，ak－(ak＋1＋ak＋2)仍是该数列中的某一项．
(ⅰ)求公比q；
(ⅱ)若bn＝－logan＋1(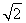
＋1)，Sn＝b1＋b2＋…＋bn，Tr＝S1＋S2＋…＋Sn，试用S2011表示T2011.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
