
【题目】某几何体的三视图如图所示,则该几何体的外接球的表面积为( )

A. 136π B. 144π C. 36π D. 34π
【答案】D
【解析】分析:作出几何体的直观图,建立空间直角坐标系,求出外接球的球心,从而可的外接球的半径,再计算出外接球的面积.
详解:由三视图可知几何体为四棱锥E﹣ABCD,直观图如图所示:
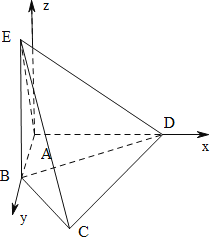
其中,BE⊥平面ABCD,BE=4,AB⊥AD,AB=![]() ,
,
C到AB的距离为2,C到AD的距离为2![]() ,
,
以A为原点,以AB,AD,及平面ABCD过A的垂线为坐标轴建立空间直角坐标系A﹣xyz,
则A(0,0,0),B(0,![]() ,0),C(2,2
,0),C(2,2![]() ,0),D(4,0,0),E(0,
,0),D(4,0,0),E(0,![]() ,4).
,4).
设外接球的球心为M(x,y,z),则MA=MB=MC=MD=ME,
∴x2+y2+z2=x2+(y﹣![]() )2+z2=(x﹣2)2+(y﹣2
)2+z2=(x﹣2)2+(y﹣2![]() )2+z2=(x﹣4)2+y2+z2=x2+(y﹣
)2+z2=(x﹣4)2+y2+z2=x2+(y﹣![]() )2+(z﹣4)2,
)2+(z﹣4)2,
解得x=2,y=![]() ,z=2.
,z=2.
∴外接球的半径r=MA=![]() =
=![]() ,
,
∴外接球的表面积S=4πr2=34π.
故选:D.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
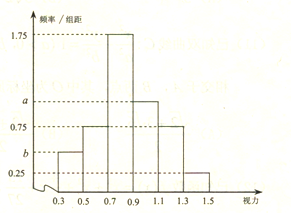
【题目】从某校高三年级中随机抽取100名学生,对其高校招生体检表中的视图情况进行统计,得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若某大学![]() 专业的报考要求之一是视力在0.9以上,则对这100人中能报考
专业的报考要求之一是视力在0.9以上,则对这100人中能报考![]() 专业的学生采用按视力分层抽样的方法抽取8人,调查他们对
专业的学生采用按视力分层抽样的方法抽取8人,调查他们对![]() 专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学
专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学![]() 专业的调查,记抽到的学生中视力在
专业的调查,记抽到的学生中视力在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 满足:
满足: ![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),证明:直线
不重合),证明:直线![]() 恒过定点,并求该定点的坐标.
恒过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“三个臭皮匠,赛过诸葛亮”,这是我们常说的口头禅,主要是说集体智慧的强大. 假设李某智商较高,他独自一人解决项目M的概率为![]() ;同时,有
;同时,有![]() 个水平相同的人也在研究项目M,他们各自独立地解决项目M的概率都是
个水平相同的人也在研究项目M,他们各自独立地解决项目M的概率都是![]() .现在李某单独研究项目M,且这
.现在李某单独研究项目M,且这![]() 个人组成的团队也同时研究项目M,设这个
个人组成的团队也同时研究项目M,设这个![]() 人团队解决项目M的概率为
人团队解决项目M的概率为![]() ,若
,若![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年中央电视台春节联欢晚会分会场之一落户黔东南州黎平县肇兴侗寨,黔东南州某中学高二社会实践小组就社区群众春晚节目的关注度进行了调查,随机抽取80名群众进行调查,将他们的年龄分成6段: ![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图.问:
,得到如图所示的频率分布直方图.问:

(Ⅰ)求这80名群众年龄的中位数;
(Ⅱ)若用分层抽样的方法从年龄在![]() 中的群众随机抽取6名,并从这6名群众中选派3人外出宣传黔东南,求选派的3名群众年龄在
中的群众随机抽取6名,并从这6名群众中选派3人外出宣传黔东南,求选派的3名群众年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为A,直线
的圆心为A,直线![]() 过点B(1,0)且与
过点B(1,0)且与![]() 轴不重合,
轴不重合,![]() 交圆A于C,D两点,过B作AC的平行线交AD于点E.
交圆A于C,D两点,过B作AC的平行线交AD于点E.
(Ⅰ)证明:![]() 为定值,并写出点E的轨迹方程;
为定值,并写出点E的轨迹方程;
(Ⅱ)设点E的轨迹为曲线C1,直线![]() 交C1于M,N两点,过B且与
交C1于M,N两点,过B且与![]() 垂直的直线与C1交于P,Q两点, 求证:
垂直的直线与C1交于P,Q两点, 求证:![]() 是定值,并求出该定值.
是定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每月生产某种产品四件,经检测发现,工厂生产该产品的合格率为![]() ,已知生产一件合格品能盈利100万元,生产一件次品将会亏损50万元,假设该产品任何两件之间合格与否相互没有影响.
,已知生产一件合格品能盈利100万元,生产一件次品将会亏损50万元,假设该产品任何两件之间合格与否相互没有影响.
(1)若该工厂制定了每月盈利额不低于250万元的目标,求该工厂达到盈利目标的概率;
(2)求工厂每月盈利额![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com