
����Ŀ��Ϊӭ��![]() ��
��![]() �յġ�ȫ�����ա���ij��ѧѧ�����ȫ�������������ȡ
�յġ�ȫ�����ա���ij��ѧѧ�����ȫ�������������ȡ![]() �������μ�
�������μ�![]() ���г��ܲ��ԣ������Եõ�ÿ���������ܲ�����ʱ��ľ�Ҷͼ��С����ǰһλ����Ϊ����С����ĺ�һλ����ΪҶ������ͼ�����ܲ�ʱ�䲻����
���г��ܲ��ԣ������Եõ�ÿ���������ܲ�����ʱ��ľ�Ҷͼ��С����ǰһλ����Ϊ����С����ĺ�һλ����ΪҶ������ͼ�����ܲ�ʱ�䲻����![]() �룬���Ϊ�������ܡ�.
�룬���Ϊ�������ܡ�.
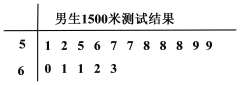
���� д���������ݵ���������λ����
����Ҫ���� ![]() �������ѡȡ
�������ѡȡ![]() �ˣ���������
�ˣ���������![]() ���ǡ������ܡ��ĸ��ʣ�
���ǡ������ܡ��ĸ��ʣ�
�������� ![]() �˵�������������������ѧУ�������������ݣ����Ӹ�У�����������ڶࣩ��ȡ
�˵�������������������ѧУ�������������ݣ����Ӹ�У�����������ڶࣩ��ȡ![]() �ˣ���
�ˣ���![]() ��ʾ�鵽�������ܡ�ѧ������������
��ʾ�鵽�������ܡ�ѧ������������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
���𰸡�(1) �������ݵ���������λ���ֱ���![]() .
.
(2) ![]() .
.
(3)�ֲ��м�������![]() .
.
������������������������������λ���Ķ���д���������ݵ���������λ��. �������ùŵ������������![]() ���ǡ������ܡ��ĸ���. �������ö���ֲ���
���ǡ������ܡ��ĸ���. �������ö���ֲ���![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
��⣺��I���������ݵ���������λ���ֱ���![]() ��
��
��II������������![]() ���ǡ������ܡ����¼�ΪA,���¼�A�����û����¼�����Ϊ;
���ǡ������ܡ����¼�ΪA,���¼�A�����û����¼�����Ϊ;
![]() �ܵĻ����¼�����Ϊ
�ܵĻ����¼�����Ϊ![]() ��
��![]()
���� ![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]()
���ڸ�У���������ڶ࣬��![]() ���Ʒ��Ӷ���ֲ�
���Ʒ��Ӷ���ֲ�![]()
![]() ��
��![]() ,
,![]() ,
,![]()
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
|
|
|
��![]() ����ѧ����
����ѧ����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() �����Σ�
������![]() ��
��![]() ��
��![]() ��
��![]() .
.
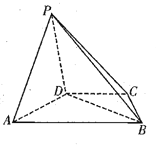
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��ƽ��
��ƽ��![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ��
��![]() �����
�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����FΪ������C��y2=4x�Ľ��㣬����P����1��0����ֱ��l��������C������A��B����QΪ�߶�AB���е㣬��|FQ|=2����ֱ��l��б�ʵ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й����ʽ��ڲ�������2018��11��5�ա�10�����Ϻ����һ�չ���ľٰ졣�����ڼ�,ij��˾���ɹ�������ijˮ����ֲ���ص�ˮ������˾���ܾ��������ֲ���صĸ����˳��ϰ��̶�һ���Բɹ�һ��ˮ���IJɹ���![]() ��Ԫ/�֣���ɹ���
��Ԫ/�֣���ɹ���![]() ���֣�֮��ĺ�����ϵ��ͼ����ͼ�е�����
���֣�֮��ĺ�����ϵ��ͼ����ͼ�е�����![]() ��ʾ���������˵�
��ʾ���������˵�![]() ���������˵�
���������˵�![]() ��.
��.

������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
������֪��ˮ����ֲ������ֲ��ˮ���ijɱ���2800Ԫ/�֣���ô���ܾ����IJɹ���Ϊ����ʱ����ˮ��������������������������![]() �����������Ƕ��٣�
�����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ϵĺ���
�ϵĺ���![]() ��������㣺������
��������㣺������![]() �����ڳ���
�����ڳ���![]() ������
������![]() ���������
���������![]() ��
��![]() �ϵ��н纯��������
�ϵ��н纯��������![]() ��Ϊ����
��Ϊ����![]() ��һ���Ͻ�����֪����
��һ���Ͻ�����֪����![]() ��
��![]() ��
��
��1��������![]() Ϊ�溯������ʵ��
Ϊ�溯������ʵ��![]() ��ֵ��
��ֵ��
��2���ڣ�1����������������![]() ������
������![]() �ϵ������Ͻ繹�ɵļ��ϣ�
�ϵ������Ͻ繹�ɵļ��ϣ�
��3��������![]() ��
��![]() ������5Ϊ�Ͻ���н纯������ʵ��
������5Ϊ�Ͻ���н纯������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�� ![]() ��
�� ![]() ��
�� ![]() ���ı���
���ı���![]() Ϊ���Σ�ƽ��
Ϊ���Σ�ƽ��![]() ƽ��
ƽ��![]() ��
�� ![]() .
.

������֤�� ![]() ƽ��
ƽ��![]() ��
��
����![]() ���߶�
���߶�![]() ���˶�����ƽ��
���˶�����ƽ��![]() ��ƽ��
��ƽ��![]() ����������Ϊ
����������Ϊ![]() ������
������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�ضԽ���BD�۳�ֱ�����A��BC��C���������ĸ����ۣ�
��AC��BD���ڡ�ABC�ǵȱ������Σ�
��AB��CD���ɵĽ�90�㣻�ܶ����A��BC��D��ƽ�������ֵ��![]() ��
��
������ȷ������ ����д��������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ǵȲ����У�����
�ǵȲ����У�����![]() ��
�� ![]() ������
������![]() ����
����![]() ��
�� ![]() ����
����![]() �ǵȱ�����.
�ǵȱ�����.
��1��������![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2��������![]() ��ǰ
��ǰ![]() ���.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������12�֣���֪��Բ![]() ����
����![]() ����������Ϊ
����������Ϊ![]() .
.
����������Բ![]() �ķ��̣�
�ķ��̣�
������![]() Ϊ��Բ
Ϊ��Բ![]() �����Ҷ��㣬ֱ��
�����Ҷ��㣬ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ����Բ
����Բ![]() ������
������
![]() �Ķ��㣬ֱ��
�Ķ��㣬ֱ��![]() �ֱ�ֱ��
�ֱ�ֱ��![]() ��
��![]() ����.֤����
����.֤����![]() ��Ϊ��ֵ.
��Ϊ��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com