
【题目】已知圆![]() 经过点
经过点![]() 和
和![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1)求圆![]() 的方程.
的方程.
(2)设直线![]() 经过点
经过点![]() ,且
,且![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() ,或
,或![]() .
.
【解析】试题分析:(1)根据圆心在直线x-y+1=0上,设出圆心坐标,设出圆的半径,得到圆的标准方程,然后把点A,B的坐标代入圆的方程,求解方程组即可得到待求系数,则方程可求;
(2)分斜率存在和不存在写出切线方程,当斜率不存在时,验证知符合题意,当斜率存在时,利用圆心到直线的距离等于半径可求k的值,所以圆的切线方程可求.
试题解析:
(1)因为圆心![]() 在直线
在直线![]() 上,所以设圆
上,所以设圆![]() 的圆心
的圆心![]() ,半径为
,半径为![]() ,
,
所以圆的方程为![]() .
.
因为圆![]() 经过点
经过点![]() ,
, ![]() ,
,
所以, 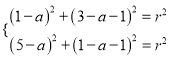 即
即![]() ,
,
解得: ![]() .
.
所以,圆![]() 的方程为
的方程为![]() .
.
(2)由题意设直线![]() 的方程为
的方程为![]() ,或
,或![]() ,
,
当![]() 的方程为
的方程为![]() 时,验证知
时,验证知![]() 与圆
与圆![]() 相切,
相切,
当![]() 的方程为
的方程为![]() ,即
,即![]() 时,
时,
圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,解得:
,解得: ![]() .
.
所以, ![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
所以,直线![]() 的方程为
的方程为![]() ,或
,或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】将一枚质地均匀且四个面上分别标有1,2,3,4的正四面体先后抛掷两次,其底面落于桌面上,记第一次朝下面的数字为![]() ,第二次朝下面的数字为
,第二次朝下面的数字为![]() .用
.用![]() 表示一个基本事件.
表示一个基本事件.
请写出所有基本事件;
求满足条件“![]() ”为整数的事件的概率;
”为整数的事件的概率;
求满足条件“![]() ”的事件的概率.
”的事件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.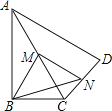
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为
②该函数的一条性质:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)已知点A的坐标为(1,0),
①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为 ![]() ,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() 为参数). 点
为参数). 点![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考浙江文数】如图,设抛物线![]() 的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.
的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.
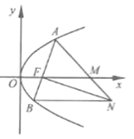
(I)求p的值;
(II)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x
轴交于点M.求M的横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com