
【题目】给出下列命题:①等比数列1,![]() ,
,![]() ,
,![]() ,…(
,…(![]() )的前
)的前![]() 项和为
项和为![]() ;②等差数列
;②等差数列![]() 中,若
中,若![]() ,
,![]() ,则该数列的前13项或14项之和最大;③若等差数列
,则该数列的前13项或14项之和最大;③若等差数列![]() 公差为
公差为![]() ,则其前
,则其前![]() 项和
项和![]() ;④若等比数列
;④若等比数列![]() 单调递增的充要条件是首项
单调递增的充要条件是首项![]() ,且公比
,且公比![]() ;⑤若数列
;⑤若数列![]() 满足
满足![]() ,
,![]() ,则
,则![]() .其中正确的是______(把你认为正确的命题序号都填上).
.其中正确的是______(把你认为正确的命题序号都填上).
【答案】②③⑤
【解析】
当![]() 时可判断出①;在②中,由已知条件结合等差数列的性质易得
时可判断出①;在②中,由已知条件结合等差数列的性质易得![]() ,根据等差数列前
,根据等差数列前![]() 项和的性质即可得出结论;在③中,利用等差数列的前
项和的性质即可得出结论;在③中,利用等差数列的前![]() 项和公式和通项公式即可得结果;在④中,当
项和公式和通项公式即可得结果;在④中,当![]() ,
,![]() 时,等比数列也为递增,可判断④;在⑤中,可判断出数列
时,等比数列也为递增,可判断④;在⑤中,可判断出数列![]() 为等差数列,求出其通项公式并判断出其与0的关系,代入即可得结论.
为等差数列,求出其通项公式并判断出其与0的关系,代入即可得结论.
对于①,当![]() 时,显然不成立;
时,显然不成立;
对于②,由于![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴该数列的前13项或14项之和最大,故②正确;
对于③,由于![]() ,
,
∴![]() ,故③正确.
,故③正确.
对于④,由于等比数列的通项公式为![]() ,
,
故当![]() ,
,![]() 时,等比数列也为递增数列,故④错误;
时,等比数列也为递增数列,故④错误;
对于⑤,由于![]() ,
,![]() ,
,
∴数列![]() 是以
是以![]() 为首项,2为公差的等差数列,
为首项,2为公差的等差数列,
∴![]() ,
,
即可得当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() ,故⑤正确;
,故⑤正确;
故答案为:②③⑤.


科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所.现采用分层抽样的方法从这些学校中抽取6所学校,对学生进行视力检查.
(Ⅰ) 求应从小学、中学、大学中分别抽取的学校数目;
(Ⅱ) 若从抽取的6所学校中随即抽取2所学校作进一步数据
①列出所有可能抽取的结果;
②求抽取的2所学校没有大学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
说明你的理由;

(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的![]() 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为
个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为![]() ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当![]() 取何值时,有3个坑要补播种的概率最大?最大概率为多少?
取何值时,有3个坑要补播种的概率最大?最大概率为多少?
(2)当![]() 时,用
时,用![]() 表示要补播种的坑的个数,求
表示要补播种的坑的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三个命题:(1)如果一个平面内有无数条直线平行于另一个平面,则这两个平面平行;(2)一个平面内的任意一条直线都与另一个平面不相交,则这两个平面平行;(3)一个平面内有不共线的三点到另一个平面的距离相等,则这两个平面平行;其中正确命题的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据得到如图所示的频率分布直方图.若尺寸落在区间(![]() )之外,则认为该零件属“不合格”的零件,其中
)之外,则认为该零件属“不合格”的零件,其中![]() ,分别为样本平均数和样本标准差,计算可得:
,分别为样本平均数和样本标准差,计算可得:![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).

(1)若一个零件的尺寸是![]() ,试判断该零件是否属于“不合格”的零件;
,试判断该零件是否属于“不合格”的零件;
(2)工厂利用分层抽样的方法从样本的前3组中抽出6个零件,标上记号,并从这6个零件中再抽取2个,求再次抽取的2个零件中恰有1个尺寸不超过![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是
是![]() 且边长为
且边长为![]() 的菱形,侧面
的菱形,侧面![]() 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面![]() ,若
,若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
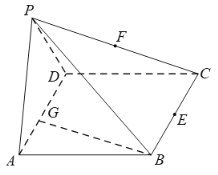
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() ,若存在,确定点
,若存在,确定点![]() 的位置;若不存在,说明理由
的位置;若不存在,说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com