
过抛物线y2=4x上一点A(1,2)作抛物线的切线,分别交x轴于点B,交y轴于点D,点C(异于点A)在抛物线上,点E在线段AC上,满足![]() =λ1
=λ1![]() ;点F在线段BC上,满足
;点F在线段BC上,满足![]() =λ2
=λ2![]() ,且λ1+λ2=1,线段CD与EF交于点P.
,且λ1+λ2=1,线段CD与EF交于点P.
(1)设![]() ,求
,求![]() ;
;
(2)当点C在抛物线上移动时,求点P的轨迹方程.

解:(1)过点A的切线方程为y=x+1. …………………………………………………1分
切线交x轴于点B(-1,0),交y轴交于点D(0,1),则D是AB的中点.
所以![]() . (1) ………………………3分
. (1) ………………………3分
由![]() Þ
Þ![]() =(1+λ)
=(1+λ)![]() Þ
Þ![]() . (2)
. (2)
同理由 ![]() =λ1
=λ1![]() , 得
, 得![]() =(1+λ1)
=(1+λ1)![]() , (3)
, (3)
![]() =λ2
=λ2![]() , 得
, 得![]() =(1+λ2)
=(1+λ2)![]() . (4)
. (4)
将(2)、(3)、(4)式代入(1)得![]() .
.
因为E、P、F三点共线,所以 ![]() +
+ ![]() =1,
=1,
再由λ1+λ2=1,解之得λ=![]() .……………………………………………………………6分
.……………………………………………………………6分
(2)由(1)得CP=2PD,D是AB的中点,所以点P为△ABC的重心.
所以,x=![]() ,y=
,y=![]() .
.
解得x0=3x,y0=3y-2,代入y02=4x0得,(3y-2)2=12x.
由于x0≠1,故x≠3.所求轨迹方程为(3y-2)2=12x (x≠3). ………………………10分


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
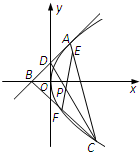 过抛物线y2=4x上一点A(1,2)作抛物线的切线,分别交x轴于点B,交y轴于点D,点C(异于点A)在抛物线上,点E在线段AC上,满足
过抛物线y2=4x上一点A(1,2)作抛物线的切线,分别交x轴于点B,交y轴于点D,点C(异于点A)在抛物线上,点E在线段AC上,满足| AE |
| EC |
| BF |
| FC |
| DP |
| PC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图:过抛物线y2=4x上的点A(1,2)作切线l交x轴与直线x=-4分别于D,B.动点P是抛物线y2=4x上的一点,点E在线段AP上,满足
如图:过抛物线y2=4x上的点A(1,2)作切线l交x轴与直线x=-4分别于D,B.动点P是抛物线y2=4x上的一点,点E在线段AP上,满足| AE |
| EP |
| BF |
| FP |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省高考数学仿真押题试卷(12)(解析版) 题型:解答题
 =λ1
=λ1 ;点F在线段BC上,满足
;点F在线段BC上,满足 =λ2
=λ2 ,且λ1+λ2=1,线段CD与EF交于点P.
,且λ1+λ2=1,线段CD与EF交于点P. ,求λ;
,求λ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com