
【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
【答案】见解析
【解析】
(1)证明 求函数f(x)的导数
f′(x)=ax2-2bx+2-b.
由函数f(x)在x=x1处取得极大值,
在x=x2处取得极小值,
知x1、x2是f′(x)=0的两个根,
所以f′(x)=a(x-x1)(x-x2).
当x<x1时,f(x)为增函数,f′(x)>0,
由x-x1<0,x-x2<0得a>0.
(2)解 在题设下,0<x1<1<x2<2等价于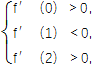
即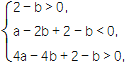 化简得
化简得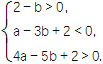
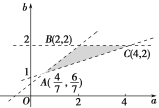
此不等式组表示的区域为平面aOb上的三条直线:
2-b=0,a-3b+2=0,4a-5b+2=0所围成的△ABC的内部,其三个顶点分别为A![]() ,B(2,2),C(4,2).
,B(2,2),C(4,2).
z在这三点的值依次为![]() ,6,8.
,6,8.
所以z的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,求数列
,求数列![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _________,
_________, ![]() __________,
__________, ![]() _________.
_________.
猜想: ![]() _______.
_______.
然后用数学归纳法证明.证明过程如下:
①当![]() 时,________________,猜想成立
时,________________,猜想成立
②假设![]() (
(![]() N*)时,猜想成立,即
N*)时,猜想成立,即![]() _______.
_______.
那么,当![]() 时,由已知
时,由已知![]() ,得
,得![]() _________.
_________.
又![]() ,两式相减并化简,得
,两式相减并化简,得![]() _____________(用含
_____________(用含![]() 的代数式表示).
的代数式表示).
所以,当![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何![]() N*都成立.
N*都成立.
思路2:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _____________.
_____________.
由已知![]() ,写出
,写出![]() 与
与![]() 的关系式:
的关系式: ![]() _____________________,
_____________________,
两式相减,得![]() 与
与![]() 的递推关系式:
的递推关系式: ![]() ____________________.
____________________.
整理: ![]() ____________.
____________.
发现:数列![]() 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.
得出:数列![]() 的通项公式
的通项公式![]() ____,进而得到
____,进而得到![]() ____________.
____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关心的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 |
|
|
|
|
|
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 |
|
|
|
|
|
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在![]() ,
,![]() 的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在![]() 的被调查者中选取的2人都赞成“延迟退休”的概率;
的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①![]() ;②当
;②当![]() 时,
时, ![]() ;③
;③![]() ;④当
;④当![]() 秒时,
秒时, ![]() ∽
∽![]() ;⑤当
;⑤当![]() 的面积为
的面积为![]() 时,时间
时,时间![]() 的值是
的值是![]() 或
或![]() ;其中正确的结论是( )
;其中正确的结论是( )
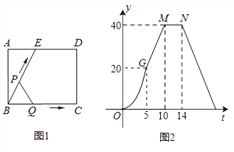
A. ①⑤ B. ②⑤ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
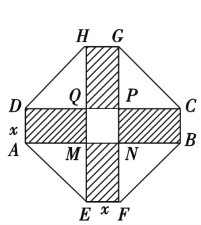
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)计算上线考生中抽取的男生成绩的方差![]() ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)
(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
R(x)=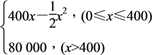
其中x是仪器的月产量.
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少元?(总收益=总成本+利润)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名;乙协会的运动员
名;乙协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名.从这
名.从这![]() 名运动员中随机选择
名运动员中随机选择![]() 人参加比赛.
人参加比赛.
(1)设![]() 为事件“选出的
为事件“选出的![]() 人中恰有
人中恰有![]() 名种子选手,且这
名种子选手,且这![]() 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出的
为选出的![]() 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com