
【题目】高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设![]() ,用
,用![]() 表示不超过x的最大整数,则
表示不超过x的最大整数,则![]() 称为高斯函数,例如:
称为高斯函数,例如:![]() ,
,![]() .已知函数
.已知函数![]() ,则关于函数
,则关于函数![]() 的叙述中正确的是( )
的叙述中正确的是( )
A.![]() 是偶函数B.
是偶函数B.![]() 是奇函数
是奇函数
C.![]() 在R上是增函数D.
在R上是增函数D.![]() 的值域是
的值域是![]()
E.![]() 的值域是
的值域是![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
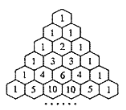
【题目】“杨辉三角”是我国数学史上的一个伟大成就,是二项式系数在三角形中的一种几何排列.如图所示,去除所有为1的项,依此构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前46项和为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了100名魔方爱好者进行调查,得到的部分数据如表所示:已知在全部100人中随机抽取1人抽到喜欢盲拧的概率为![]() .
.
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | 10 | ||
女 | 20 | ||
总计 | 100 |
表(1)
并邀请这100人中的喜欢盲拧的人参加盲拧三阶魔方比赛,其完成时间的频率分布如表所示:
完成时间(分钟) | [0,10) | [10,20) | [20,30) | [30,40] |
频率 | 0.2 | 0.4 | 0.3 | 0.1 |
表(2)
(Ⅰ)将表(1)补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表(2)中完成时间在[30,40] 内的人中任意抽取2人对他们的盲拧情况进行视频记录,记完成时间在[30,40]内的甲、乙、丙3人中恰有一人被抽到为事件A,求事件A发生的概率.
(参考公式: ,其中
,其中![]() )
)
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:①若m![]() α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.其中真命题的个数是( )
α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.其中真命题的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次诗词大会决赛前,甲、乙、丙丁四位选手有机会问鼎冠军,![]() 三名诗词爱好者依据选手在之前比赛中的表现,结合自己的判断,对本场比赛的冠军进行了如下猜测:
三名诗词爱好者依据选手在之前比赛中的表现,结合自己的判断,对本场比赛的冠军进行了如下猜测:![]() 猜测冠军是乙或丁;
猜测冠军是乙或丁;![]() 猜测冠军一定不是丙和丁;
猜测冠军一定不是丙和丁;![]() 猜测冠军是甲或乙。比赛结束后发现,
猜测冠军是甲或乙。比赛结束后发现,![]() 三个人中只有一个人的猜测是正确的,则冠军是( )
三个人中只有一个人的猜测是正确的,则冠军是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知直线
轴正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并指出该曲线是什么曲线;
的直角坐标方程,并指出该曲线是什么曲线;
(2)若直线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com