
【题目】如图,四棱锥P-ABCD的底面是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.

(Ⅰ)设![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() //平面
//平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)思路一:先证明直线![]() 所在平面与平面
所在平面与平面![]() 平行,再根据面面平行的定义说明直线
平行,再根据面面平行的定义说明直线![]() 与平面
与平面![]() 平行.取
平行.取![]() 中点
中点![]() ,连接
,连接![]() ,易证平面
,易证平面![]() 与平面
与平面![]() 平行,从而问题得证;思路二:利用线面平行的判定定理来证明,取
平行,从而问题得证;思路二:利用线面平行的判定定理来证明,取![]() 中点
中点![]() ,连接
,连接![]() ,易证四边形
,易证四边形![]() 为平行四边形,则
为平行四边形,则![]() ∥
∥![]() ,从而问题可得证.(Ⅱ)根据题意,利用“坐标法”来解决,建立适当的空间直角坐标系,通过向量数量积的坐标运算,从而可得解.
,从而问题可得证.(Ⅱ)根据题意,利用“坐标法”来解决,建立适当的空间直角坐标系,通过向量数量积的坐标运算,从而可得解.
试题解析:(Ⅰ)证明:设线段![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() . 在△
. 在△![]() 中,
中,![]() 为中位线,故
为中位线,故![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
在底面直角梯形![]() 中,
中,![]() ,且
,且![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,
即![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,所以平面
,所以平面![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
所以有![]() 平面
平面![]() .
.
(Ⅱ)如图所示,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系.
轴正方向,建立空间直角坐标系.

设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() ,即
,即![]() ,
,
可取![]() ,同理,设
,同理,设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() ,可取
,可取![]() ,
,
从而![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“中国式过马路”的大意是凑够一撮人即可走,跟红绿灯无关.部分法律专家的观点为“交通规则的制定目的就在于服务城市管理,方便行人,而‘中国式过马路’是对我国法治化进程的严重阻碍,反应了国人规则意识的淡薄.”某新闻媒体对此观点进行了网上调查,所有参与调查的人中,持“支持”“中立”和“不支持”态度的人数如表所示:
支持 | 中立 | 不支持 | |
20岁以下 | 800 | 450 | 200 |
20岁及以上 | 100 | 150 | 300 |
在所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,已知从持“支持”态度的人抽取了45人,则
人,已知从持“支持”态度的人抽取了45人,则![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年消毒液和口罩成了抢手年货,老百姓几乎人人都需要,但对于![]() 这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于
这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于![]() 这种口罩了解的占
这种口罩了解的占![]() ,其中45岁以上(含45岁)的人数占
,其中45岁以上(含45岁)的人数占![]() .
.
(1)将答题卡上的列联表补充完整;
(2)判断是否有![]() 的把握认为对
的把握认为对![]() 这种口罩的了解与否与年龄有关.
这种口罩的了解与否与年龄有关.
参考公式: ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,各个侧面均是边长为
中,各个侧面均是边长为![]() 的正方形,
的正方形,![]() 为线段
为线段![]() 的中点.
的中点.
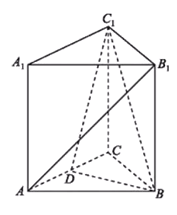
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)设![]() 为线段
为线段![]() 上任意一点,在
上任意一点,在![]() 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长分别为a,b,c,有以下四个命题:
的三边长分别为a,b,c,有以下四个命题:
①以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
②以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
③以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
④以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在.
为边长的三角形一定存在.
其中正确的命题为( )
A.①③B.②③C.②④D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com