
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 距离之和的最小值为( )
距离之和的最小值为( )
A. 1 B. 2 C. 3 D. 4
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:
【题目】已知如图1,在Rt△ABC中,∠ACB=30°,∠ABC=90°,D为AC中点,AE![]() BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD
BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD![]() 平面BCD,如图2所示。
平面BCD,如图2所示。
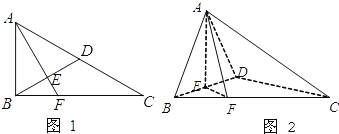
(Ⅰ)求证:AE![]() 平面BCD;
平面BCD;
(Ⅱ)求二面角A-DC-B的余弦值;
(Ⅲ)求三棱锥B-AEF与四棱锥A-FEDC的体积的比(只需写出结果,不要求过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于非负整数集合![]() (非空),若对任意
(非空),若对任意![]() ,或者
,或者![]() ,或者
,或者![]() ,则称
,则称![]() 为一个好集合.以下记
为一个好集合.以下记![]() 为
为![]() 的元素个数.
的元素个数.
(1)给出所有的元素均小于![]() 的好集合.(给出结论即可)
的好集合.(给出结论即可)
(2)求出所有满足![]() 的好集合.(同时说明理由)
的好集合.(同时说明理由)
(3)若好集合![]() 满足
满足![]() ,求证:
,求证:![]() 中存在元素
中存在元素![]() ,使得
,使得![]() 中所有元素均为
中所有元素均为![]() 的整数倍.
的整数倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体![]() ,这个几何体的体积为
,这个几何体的体积为![]() .
.

(1)求棱![]() 的长;
的长;
(2)求经过![]() ,
,![]() ,
,![]() ,
,![]() 四点的球的表面积和体积.
四点的球的表面积和体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=60°,AB=PA=4,E是PA的中点,AC,BD交于点O.
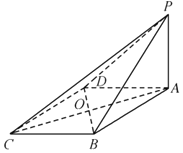
(1)求证:OE∥平面PBC;
(2)求三棱锥E﹣PBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD![]() 中,以D为原点建立空间直角坐标系,E为B
中,以D为原点建立空间直角坐标系,E为B![]() 的中点,F为
的中点,F为![]() 的中点,则下列向量中,能作为平面AEF的法向量的是( )
的中点,则下列向量中,能作为平面AEF的法向量的是( )
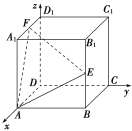
A. (1,-2,4) B. (-4,1,-2)
C. (2,-2,1) D. (1,2,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的焦距为2
的焦距为2![]() ,左顶点与上顶点连线的斜率为
,左顶点与上顶点连线的斜率为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点P(m,0)作圆x2+y2=1的一条切线l交椭圆C于M,N两点,当|MN|的值最大时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com