
【题目】已知![]() 的三个顶点
的三个顶点![]() ,其外接圆为圆
,其外接圆为圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)对于线段![]() (包括端点)上的任意一点
(包括端点)上的任意一点![]() ,若在以
,若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,求圆
的中点,求圆![]() 的半径
的半径![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]()
【解析】
试题(1)借助题设条件直接求解;(2)借助题设待定直线的斜率,再运用直线的点斜式方程求解;(3)借助题设建立关于![]() 的不等式,运用分析推证的方法进行求解.
的不等式,运用分析推证的方法进行求解.
试题解析:
(1)![]() 的面积为2;
的面积为2;
(2)线段![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,线段
,线段![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,
,
所以![]() 外接圆圆心
外接圆圆心![]() ,半径
,半径![]() ,圆
,圆![]() 的方程为
的方程为![]() ,
,
设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,因为直线
,因为直线![]() 被圆
被圆![]() 截得的弦长为2,所以
截得的弦长为2,所以![]() .
.
当直线![]() 垂直于
垂直于![]() 轴时,显然符合题意,即
轴时,显然符合题意,即![]() 为所求;
为所求;
当直线![]() 不垂直于
不垂直于![]() 轴时,设直线方程为
轴时,设直线方程为![]() ,则
,则![]() ,解得
,解得![]() ,
,
综上,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,
,
因为点![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() ,又
,又![]() ,
,![]() 都在半径为
都在半径为![]() 的圆
的圆![]() 上,
上,
所以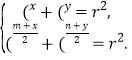 即
即![]()
因为该关于![]() ,
,![]() 的方程组有解,即以
的方程组有解,即以![]() 为圆心,
为圆心,![]() 为半径的圆与以
为半径的圆与以![]() 为圆心,
为圆心,![]() 为半径的圆有公共点,所以
为半径的圆有公共点,所以![]() ,
,
又![]() ,所以
,所以![]() 对
对![]() 成立.
成立.
而![]() 在
在![]() 上的值域为
上的值域为![]() ,所以
,所以![]() 且
且![]() .
.
又线段![]() 与圆
与圆![]() 无公共点,所以
无公共点,所以![]() 对
对![]() 成立,即
成立,即![]() .
.
故圆![]() 的半径
的半径![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且f(﹣x﹣1)=f(x﹣1),当x∈[﹣1,0]时,f(x)=﹣x3 , 则关于x的方程f(x)=|cosπx|在[﹣ ![]() ,
, ![]() ]上的所有实数解之和为( )
]上的所有实数解之和为( )
A.﹣7
B.﹣6
C.﹣3
D.﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且 ![]() =λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.
=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示. 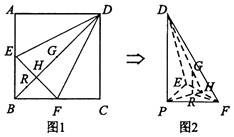
(I)若λ=2,求证:GR⊥平面PEF;
(Ⅱ)是否存在正实数λ,使得直线FR与平面DEF所成角的正弦值为 ![]() ?若存在,求出λ的值;若不存在,请说明理由.
?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD= ![]() ,则直线AD与平面BCD所成角的大小是( )
,则直线AD与平面BCD所成角的大小是( ) 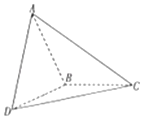
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足:Sn=nan﹣2n(n﹣1),首项![]() =1.
=1.
(1)求数列{an}的通项公式;
(2)设数列![]() 的前n项和为Mn,求证:
的前n项和为Mn,求证:![]()
![]() Mn
Mn![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com